• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Отримання допустимого базисного розв’язку

Якщо базисний розв’язок не є допустимим (ознакою цього є наявність від’ємних чисел у стовпчику вільних коефіцієнтів, що відповідають значенням базисних змінних), за допомогою симплексного методу можна поступово наближатися до області допустимих розв’язків і отримати в кінці кінців допустимий розв’язок. Для цього треба дотримуватися такого алгоритму:

1 крок. Обираємо розв’язуючий елемент:

а) в рядку з від’ємним вільним коефіцієнтом обираємо від’ємний коефіцієнт при вільних змінних – він визначає розв’язуючий стовпчик;

б) складаємо невід’ємні відношення елементів останнього стовпчика до відповідних елементів розв’язуючого стовпчика та обираємо серед них найменше – це визначає розв’язуючий рядок.

2 крок. Виконуємо алгоритм Жордана-Гауса з обраним розв’язуючим елементом.

Повторюємо кроки алгоритму доти, доки в стовпчику вільних коефіцієнтів є від’ємні числа

Приклад 7.

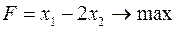
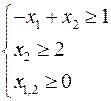
Розв’язання. Складемо симплекс-таблицю ЗЛП.

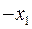
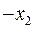
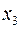
		–1	–1
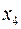
		–1	–2
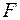
	–1

Ми маємо два від’ємних вільних коефіцієнта, тобто базисний розв’язок не є допустимим. Розглянемо, наприклад, перший рядок і оберемо в ньому від’ємний коефіцієнт при , тобто стовпчик буде розв’язуючим. Знайдемо 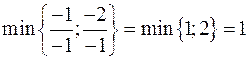, тобто рядок 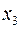буде розв’язуючим. Виконавши алгоритм Жордана-Гауса, отримуємо таблицю

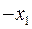
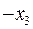
	–1	–1
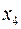
	–1	–1	–1
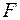
			–2

В стовпчику вільних коефіцієнтів ще залишився від’ємний елемент –1. Розглянемо цей рядок і оберемо в ньому від’ємний коефіцієнт, наприклад, при 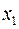. тобто стовпчик 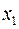буде розв’язуючим.

Знайдемо

,

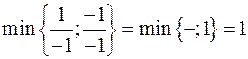тобто рядок 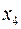буде розв’язуючим. Виконавши алгоритм Жордана-Гауса, отримуємо таблицю

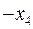
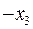
	–1
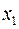
	–1
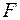
			–3

Тепер у стовпчику вільних коефіцієнтів усі елементи додатні, тобто ми отримали допустимий базисний розв’язок , , . Далі переходимо до звичайного алгоритму симплекс-методу. Критерій оптимальності вже виконаний, тобто ми маємо розв’язок задачі .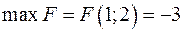

Під час відшукання допустимого базисного розв’язку може виникнути перешкода до вибору розв’язуючого стовпчика, якщо у рядку з від’ємним вільним коефіцієнтом більше немає від’ємних елементів. В цьому випадку система обмежень несумісна і ЗЛП не має розв’язку.

Читайте також:

1. Абстрактна небезпека і концепція допустимого ризику.
2. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
3. Аналогія - спосіб отримання знань про предмети та явища на основі їхньої подібності з іншими.
4. Аудит процесу продажу (реалізації продукції), циклу отримання доходів
5. Аудиторські докази: поняття та процедури отримання
6. В основу визначення витрат певного періоду покладено можливість одночасного визнання доходу, для отримання якого вони здійснені, і навпаки.
7. Валідація НАССР- отримання об'єктивного доказу того, що елементи НАССР-плану результативні.
8. Види міжнародно-правової бази у сфері прав людини і поняття міжнародного контролю за дотриманням та захистом прав людини.
9. Види процедур отримання аудиторських доказів за їх типом
10. Види процедур отримання аудиторських доказів за їх характером
11. Визначення виробляючих ліній та методи їх отримання
12. Визначення допустимого часу початку входу в зону зараження (початку роботи) за заданою дозою опромінення

Переглядів: 818