• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Нерозгалужені ланцюги

3.8.1. При послідовній сполуці елементів (мал. 4.8) мають місце такі співвідношення для миттєвих значень і комплексів напруг:

, (97)

. (98)

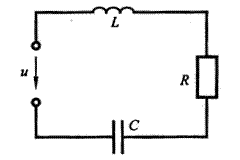
Рисунок. 3.8 Нерозгалужений електричний ланцюг.

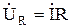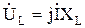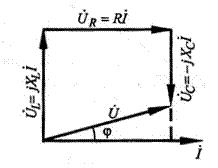
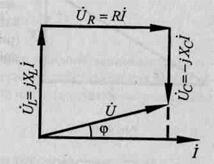
Оскільки,,, векторна діаграма має вигляд, наведений на мал. 3.9.

Рисунок. 5.9 Векторна діаграма нерозгалуженого електричного ланцюга.

3.8.2. З векторної діаграми можна записати вираження для комплексу напруги

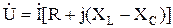, (99)

або

. (100)

Різниця X = X_L – Х_С називають реактивним опором, що в комплексній формі має вигляд

. (101)

Вираз

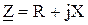, (102)

Або

, (103)

Або

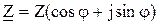. (104)

називають повним опором у комплексній формі. Модуль повного опору можна виразити як

, (105)

а j — кут між струмом і напругою визначається зі співвідношення

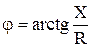. (106)

5.8.3. Прямокутний трикутник на-векторній діаграмі можна перетворити в трикутник опорів (мал. 4.10). Із трикутника опорів випливають такі співвідношення:

, (107)

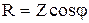, (108)

, (109)

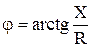. (110)

Або

. (111)

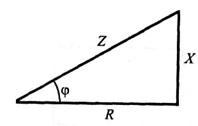
Рисунок. 3.10 Трикутник опорів.

Зрушення фаз (a) уважають позитивним, якщо wL > 1/wC.

3.8.4. Закон Ома для діючих значень і в комплексній формі для нерозгалуженого ланцюга має вигляд

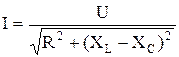,, (112)

, . (113)

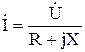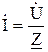, . (114)

3.8.5. Розрахунки нерозгалуженого ланцюга символічним методом можна виконувати так само, як і розрахунки ланцюга постійного струму. Якщо є ланцюг (мал. 3.11) і потрібно визначити повний опір, то можна записати співвідношення

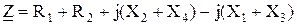. (115)

Рисунок. 3.11 Нерозгалужений електричний ланцюг з більшою кількістю елементів.

Таким чином, усі індуктивні опори множаться на символ «+j», а всі ємнісні опори множаться на символ «-j». Якщо R₁ = 3, R₂ = 2, X₁ = 1, X₂ = 3, X₃ = 2, X₄ = 4, то .

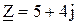Із цього випливає, що весь ланцюг можна замінити еквівалентним опором. Цей опір складається з дійсної частини (активний опір 5 Ом) і уявної частини (індуктивний реактивний опір рівний 4 Ом).

Читайте також:

1. Багатоконтурні лінійні електричні ланцюги
2. Лекція 3. Логістичні системи і ланцюги
3. Логістичні ланцюги та їх характеристика
4. Магнітні кола поділяють на нерозгалужені – однорідні та неоднорідні, і розгалужені – симетричні і несиметричні.
5. Нейрон і нейроглія як структурно-функціональні одиниці ЦНС. Нейронні ланцюги, нервові центри.
6. Нерозгалужені ланцюги перемінного струму
7. Одноконтурні лінійні електричні ланцюги
8. Прості ланцюги й методи їхнього розрахунку
9. Прості лінійні електричні ланцюги синусоїдального струму
10. СКЛАДНІ ЛАНЦЮГИ Й МЕТОДИ ЇХНЬОГО РОЗРАХУНКУ
11. Трофічні ланцюги та мережі. Трофічна структура біоценозу. Екологічні піріміди

Переглядів: 1168