• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Теорема про взаємність робіт

Розглянемо два стани пружної системи, що знаходиться в рівновазі. В кожному з цих станів на систему (споруду) діє деяке статичне навантаження, наприклад в 1-м стані сила Р₁ а в 2-м — сила Р₂ (рис. 8.3).

Переміщення системи в результаті її деформації будемо позначати D_mn, де перший індекс вказує на напрямок переміщення, а другий — на причину, що викликала його. Знак D_mn читається таким чином: переміщення по напрямку «сили.» т, викликане «.силою» п. Переміщення D_mn може бути лінійним зміщенням або кутом повороту (в радіанах) — залежно від того, чи «сила» т є зосередженою силою або зосередженим моментом.

Рис 8.3.

Під «силою» п розуміється будь-яке навантаження, яке діє на споруду, наприклад, що складається з декількох зосереджених сил і моментів і якого завгодно розподіленого навантаження. В даному випадку (рис. 8.3):

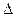₁₁-переміщення по напрямку сили Р₁ від дії сили Р₁;

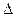_12- переміщення по напрямку сили Р₁ від дії сили Р₂;

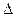₂₂- переміщення по напрямку сили Р₂ від дії сили Р₂;

- переміщення по напрямку сили 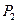від дії сили Р₁.

Тоді можна визначити величини робіт сил Р₁ і Р₂ на відповідних переміщеннях:

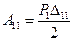- робота від дії сили Р₁ на переміщенні 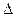₁₁;

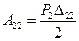- робота від дії сили Р₂ на переміщенні 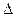₂₂.

Роботи А₁₁ та А₂₂ можна виразити через внутрішні зусилля, що виникають в поперечних перетинах стержнів системи:

;

.

Розглянемо тепер випадок статичного навантаження тієї ж системи силами P₁ і P₂ в наступній послідовності. Спочатку до системи прикладається статично наростаюча сила P₁. Коли процес її статичного наростання закінчиться, деформація системи і внутрішні зусилля, що виникають в ній, будуть такі ж, як і в 1-м стані, зображеному на рис.8.4; зокрема, прогинання під силою P₁ буде рівне А₁₁. Робота сили P₁ в процесі її наростання від

Рис. 8.4

нуля до кінцевого значення буде А₁₁=Р₁D₁₁/2. Потім на систему почне діяти також наростаюча сила Р₂- в результаті цього система отримає додаткові деформації і в ній виникнуть додаткові внутрішні зусилля, рівні деформаціям і зусиллям в 2-м стані, додаткове прогинання під силою P1 буде рівне D₁₂-в процесі наростання сили P₂ від нуля до її кінцевого значення сила P₁, залишаючись постійною, переміститься вниз на величину додаткового прогинання A₁₂ і, отже, зробить додаткову роботу,

.

Тому при послідовному завантажені робота всіх сил дорівнює:

.

З іншої сторони, роботу А сил P₁ і P₂ можна визначити як півсуму добутків кожної з цих сил на відповідне їй повне переміщення від дії обох сил:

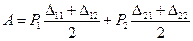
Прирівняємо два вирази і одержимо:

,

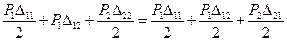звідки

,

де - 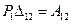- робота сили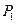- 1-го стану на переміщенні по її напрямку від дії сили 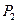другого стану;

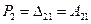- робота сили 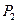2-го стану на переміщенні по її напрямку від дії сили 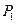першого стану.

Значить,

.

Таким чином, робота сил 1-го стану на переміщеннях по їх напрямках, викликаних силами 2-го стану, дорівнює роботі сил 2-го стану на переміщеннях по їх напрямках, викликаних силами 1-го стану - теореми про взаємність робіт, або теореми Бетті.

На основі цієї теореми можна визначити роботу 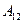через внутрішні зусилля, які виникають в першому та другому стані і при цьому отримуємо:

.8.3. Теорема про взаємність переміщень

Розглянемо наступні два стани системи. В першому стані до системи прикладена одна сила P₁ = 1, а в другому — одна сила Р₂ = 1 Ці стани системи умовимося називати одиничними. Будемо позначати переміщення, викликані одиничними силами або моментами (тобто силами Р == 1 або моментами М = 1), знаком δ — на відміну від переміщень, викликаних силами і моментами, не рівними одиниці, що позначаються знаком D. Відповідно до цього переміщення даної системи по напряму одиничної сили Р₂ в 1-м стані (тобто викликане силою P₁ = 1, позначимо δ₁₂ переміщення по напрямку одиничної сили P₁ в 2-м стані позначимо δ₂₁ де δ₁₂ і δ₂₁—одиничні переміщення.

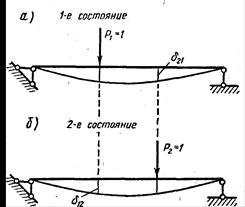
Рис. 8.5

На підставі теореми про взаємність робіт для розглядуваних двох станів маємо:

P₁δ₁₂ = P₂δ₂₁

але так ,як

P₁ = P₂=1

то

δ₁₂ = δ_21..

Або в загальному випадку дії будь-яких одиничних сил:

δ_mn = δ_nm.

Отримана рівність носить назву теореми про взаємність переміщень (принципу Максвелла): для двох одиничних станів пружної системи переміщення по напряму першої одиничної сили, викликане другою одиничною силою, дорівнює переміщенню по напряму другої сили, викликаному першою силою.

Читайте також:

1. Автоматизація проектних робіт
2. Аналіз продуктивності праці й заробітної плати
3. Аналіз фонду заробітної плати.
4. Аналіз якості продукції та робіт
5. Антиінфляційна політика. Взаємозв’язок інфляції та безробіття.
6. Аудит витрат на виробництво продукції, виконання робіт, надання послуг
7. Аудит готової продукції та продажу товарів, робіт та послуг
8. Безпека виконання робіт.
9. Безпека під час вантажно –розвантажувальних робіт.
10. Безпека під час робіт з пересувними електростанціями і колійним електричним інструментом.
11. Безробітні можуть відбувати це покарання і в нічний час.
12. Безробітні та їх правовий захист і статус

Переглядів: 2589