Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Гармонічні коливання та їх основні параметри

Розглянемо пружинний маятник (мал. 1.21). При зміщенні матеріальної точки масою т на відстань х відносно положення рівноваги на неї починає діяти сила пружності, яка викликана деформацією пружини

F_np = -kx. (1.35)

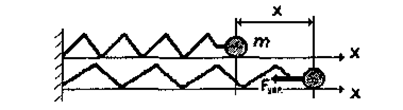
Мал. 1.21. Пружинний маятник.

Згідно з II законом Ньютона ця сила надаватиме матеріальній точці прискорення :

F_np = ma. (1.36)

Прирівнюючи праві частини рівностей (1.35) і (1.36), одержимо:

ma = -kx. (1.37)

Враховуючи, що прискорення є другою похідною від координати за часом a = х, останнє рівняння набуває вигляду лінійного диференційного рівняння

m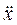+kx=0. (1.38)

Оскільки коефіцієнт жорсткості пружини k > 0 і т > 0, відношення k/m можна позначити через квадрат деякої величини ω₀: ω₀²=k/m. Тоді рівняння (1.38) матиме вигляд:

. (1.39)

Таким чином, функція х =f(t) задовольняє диференційному рівнянню ІІ-го порядку, яке є лінійним, однорідним і зі сталими коефіцієнтами. Розв'язок таких рівнянь, як відомо, зводиться до розв'язування відповідних характеристичних алгебраїчних рівнянь.

Складемо характеристичне рівняння, що відповідає ди-ференційному рівнянню (1.39):

λ²+ω₀²=0. (1.40)

Корені цього квадратного рівняння дорівнюють λ_1,2 = ±ω₀ , тобто вони є різними й уявними.

Загальний розв'язок диференційного рівняння (1.39) на випадок таких коренів відповідного характеристичного рівняння має вигляд:

x(t) = с₁ sinω₀t + с2 cosω₀t.

Нехай с₁ = Acosφ₀, а с₂ = - А sinφ₀, де А та φ₀ - довільні сталі, тоді

x(t) = Acosφ₍₎ cosω₀t- Asinφ sinωt= Acos(ω₀t + φ₀). (1.41)

Якщо покласти с₁ = A sinφ₀, а с₂ = А cosφ₀, то прийдемо до результату:

x(t) = Asin(ω₀_t + φ₀). (1.42)

Значення сталих А та φ₀ визначаються початковими умовами, тобто положенням та швидкістю матеріальної точки в момент часу t = 0.

Отже, ми дійшли до висновку: матеріальна точка, що знаходиться під дією пружної сили, здійснює коливальний рух, при якому її зміщення від положення рівноваги змінюється з часом за законом синуса або косинуса. Такі коливання називають гармонічними.

Стала А в рівняннях (1.42) є амплітуда гармонічного коливання, вона дорівнює максимальному зміщенню маятника від положення рівноваги. Аргумент синуса (або косинуса): φ(t) = ω₀t + φ₀ - фаза коливань. Фаза визначає зміщення маятника в будь-який момент часу, φ₀- початкова фаза, яка визначає зміщення маятника в момент часу t = 0.

Величина ω₀=- циклічна частота коливань.

Тій же самій закономірності підпорядковується зміщення від положення рівноваги математичного маятника, що коливається, при невеликих кутах відхилення а (мал. 1.22).

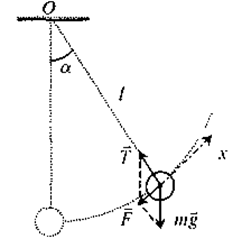
Мал. 1.22. Математичний маятник.

Сила, яка спричиняє коливання математичного маятника, не є пружна за своєю природою. Дійсно, повертаюча сила F спрямована по дотичній до дуги кола радіуса l, напрямлена до положення рівноваги і пропорційна зміщенню х:

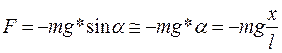
(оскільки для малих кутів α маємо ).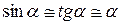

Сила, що не є пружною за своєю природою, але аналогічна їй по залежності від зміщення, називається квазіпружною. Таким чином, F є квазіпружною силою. Рівняння динаміки для математичного маятника матиме вигляд:

, або (1.43)

Отримане рівняння повністю збігається з рівнянням (1.41), що описує рух пружного маятника, а отже має той самий розв'язок. Таким чином, гармонічні коливання - це коливання, що відбуваються під дією пружних або квазіпружних сил.

Швидкість та прискорення при гармонічних коливаннях

Нехай відлік часу обрано таким чином, щоб початкова фаза φ₀= 0. Тоді розв'язок рівняння (1.41) матиме вигляд:

x(t) = Asinω₀ t. (1.44)

Швидкість тіла, що коливається, знайдемо як похідну від координати х за часом t

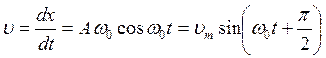, (1.45)

де υ_m = aω₀ - амплітуда швидкості.

З рівнянь (1.43) та (1.44) випливає, що швидкість також змінюється за гармонічним законом, а фаза швидкості відрізняється від фази зміщення на π/2, тобто в момент часу, коли х = 0, швидкість максимальна.

Оскільки швидкість при гармонічних коливаннях змінюється з часом, то цей рух характеризується прискоренням, яке знайдемо як другу похідну від зміщення х за часом

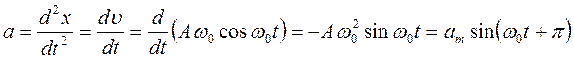(1.46)

де а_т = Аω₀² - амплітуда прискорення.

Видно, що і прискорення змінюється за гармонічним законом, а фаза прискорення відрізняється від фази зміщення на π, а від фази швидкості на π/2. Замінивши в (1.46) Asinω₀t через х, отримаємо:

a=-ω₀²x.

З цієї рівності виходить, що при гармонічних коливаннях прискорення тіла прямо пропорційне до зміщення від положення рівноваги і має протилежний зміщенню напрямок.

Період і частота гармонічних коливань

Періодом гармонічного коливального руху називають найменший проміжок часу Т, по закінченні якого всі величини, що характеризують цей рух (х, υ, а), набувають первісні значення. З рівностей (1.44) - (1.46) випливає, що періоду коливань відповідає зміна фази на величину 2π.

У момент часу t фаза дорівнює ω₀t+φ₀, а в момент часу t + Т: (ω₀(t + T) +φ₀ ). Тоді з умови періодичності (ω₀(t + T) +φ₀)- -( ω₀t+φ₀ )= 2π маємо:

. (1.47)

Підставляючи в (1.47) вирази для ω_0, що відповідають пружинному та математичному маятникам, отримаємо відповідні вирази для періодів коливань цих маятників:

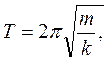
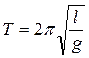(1.48)

Величину v=1/Т = ω₀/2π називають частотою коливань. Частота вказує, скільки разів за 1 сек повторюється один і той же стан тіла, що коливається. Частота вимірюється в Герцах (Гц), [v] = 1/с = с^-1 = Гц.

Розглянуті коливання відбуваються при відсутності сил тертя і зовнішніх сил. Такі коливання називають власними. Частота (період) власних коливань, як випливає з (1.48), залежить лише від властивостей самої системи.

1.3.2. Затухаючі коливання і аперіодичний рух

Припустимо, що в розглянутих системах існує тертя чи опір, причому сила тертя (опору) пропорційна швидкості: F_m=-rυ, де r - коефіцієнт тертя (опору). Запишемо в цьому випадку рівняння руху (II закон Ньютона).

ma = -kx-rυ або .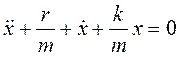

Позначивши 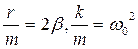,отримаємо диференційне рівняння другого порядку, що описує рух пружинного маятника у присутності сил тертя

. (1.49)

Складемо характеристичне рівняння, що відповідає ди-ференційному рівнянню (1.49):

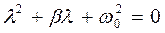Знайдемо корені характеристичного рівняння

. (1.50)

Загальний розв'язок рівняння (1.49) залежить від знака різниці β²-ω₀². Розглянемо всі можливі випадки:

1. β²<ω₀², коли корені характеристичного рівняння є комплексними числами (затухаючі коливання)

де - циклічна частота. У випадку комплексних коренів характеристичного рівняння загальний розв'язок (1.49) має вигляд

, або

, (1.51)

де A(t) = A₀e ^-β^t- амплітуда коливань, яка зменшується за експоненціальним законом, (β - коефіцієнт затухання, визначає швидкість затухання амплітуди. Залежність х = f (t) для затухаючих коливань подано на мал. 1.23.

Мал. 1.23. Затухаючі коливання.

Ступінь затухання часто характеризують декрементом затухання S і логарифмічним декрементом затухання λ*:

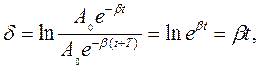
де період затухаючих коливань дорівнює

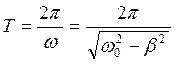
2. β²>ω₀² , коли корені характеристичного рівняння є дійсними числами (аперіодичні коливання)

У цьому випадку загальний розв'язок рівняння (1.49) матиме вигляд

(1.52)

що відповідає аперіодичному рухові (мал. 1.24).

3. β²>ω₀² , коли корені є кратними. Легко побачити, що і в цьому випадку рух тіла буде аперіодичним.

Коливання, що виникають у системі при відсутності зовнішніх сил, називають вільними. Частота вільних коливань залежить як від пружних властивостей системи (ω₀), так і від інтенсивності втрат (β). Якщо β²<<ω₀², то ω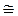ω₀ i період вільних коливань

стає близьким до періоду власних коливань (мал. 1.23).

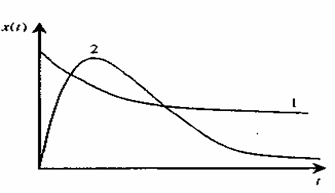
Мал. 1.24. Аперіодичний рух.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
МЕХАНІЧНІ КОЛИВАННЯ	\|	Вимушені коливання

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.008 сек.