• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Швидкість і пройдений шлях тіла під час рівноприскореного прямолінійного руху.

З визначення прискорення 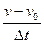випливає, що:

;

Якщо прискорення тіла спрямоване протилежно початковій швидкості тіла, то залежність модуля швидкості від часу описується формулою:

;

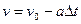Рівноприскорений рух зі зменшуваною швидкістю може тривати лише доти, доки швидкість тіла v не стане дорівнювати нулю. Час руху тіла до зупинки можна обчислити, виходячи з умови 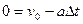. Звідси випливає, що .

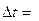
У випадку прямолінійного рівномірного руху тіла переміщення, яке здійснює це тіло, обчислюється як площа прямокутника, що міститься під графіком модуля швидкості.

І в разі прямолінійного рівноприскореного руху переміщення (або шлях) можна обчислювати за тією ж формулою, що й площу фігури під графіком швидкості.

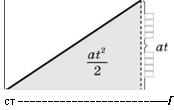
У випадку прямолінійного рівноприскореного руху без початкової швидкості залежність шляху l від часу руху t описується формулою:

,

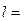
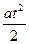де a — модуль прискорення тіла.

Слід звернути увагу на те, що в разі рівноприскореного руху без початкової швидкості шлях пропорційний квадрату часу руху.

Якщо початкова швидкість тіла не дорівнює нулю, то фігура, обмежена графіком v(t) і віссю 0t, — трапеція, що складається з прямокутника площею v₀t трикутника площею ,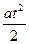

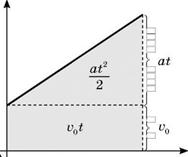
Отже, шлях можна обчислити за формулою ,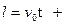

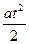Таким чином, якщо тіло рухається прямолінійно рівноприскорено з початковою швидкістю v0 і прискоренням a, то залежність шляху l від часу руху t має вигляд:

,

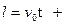
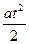якщо напрямок прискорення збігається з напрямком початкової швидкості, і вигляд:

,

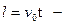
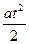якщо прискорення спрямоване протилежно напрямку початкової швидкості. Необхідно звернути увагу учнів на те, що в першому ви­падку швидкість тіла збільшується, а в другому — зменшується.

Оскільки площа трапеції дорівнює півсумі основ і висоти, то 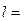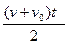. З іншого боку, 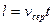. Звідси випливає, що середня швидкість у разі рівноприскореного руху дорівнює: .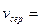

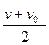З формул для шляху 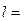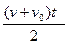і часу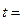 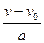дістаємо: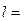 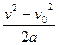. А якщо початкова швидкість дорівнює нулю, ця формула набуває вигляду: .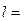

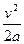Читайте також:

1. Vу -швидкість ударника
2. Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
3. Видаток і середня швидкість ламінарного потоку.
4. Вимірювання інформації та швидкість її передачі
5. Вплив параметрів режиму буріння на механічну швидкість проходки
6. Групова швидкість і дисперсія хвиль
7. Етапи, швидкість і показники адаптації
8. Закон Біо-Савара-Лапласа. Магнітне поле прямолінійного та колового струмів
9. Закон грошового обігу та швидкість обігу грошей.
10. Класифікація процесів, що протікають в продуктах під час товароруху. Їх вплив на споживчі властивості товарів
11. На скільки збільшиться маса - частинки (в а.о.м.), якщо її швидкість збільшиться від 0 до 0,9с? Вважати,що маса спокою - частинки 4 а.о.м.
12. Облік трудових ресурсів та показники його руху.

Переглядів: 8101