
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Формула для чисел Фібоначчі
Теорема 6.1. Числа Фібоначчі можна розрахувати по формулі
 .
.
Доказ. Переконаємося в справедливості цієї формули для n = 0, 1, а потім доведемо справедливість даної формули для довільного n по індукції. Обчислимо|обчислятимемо,вичислимо| відношення|ставлення| двох найближчих чисел Фібоначчі:
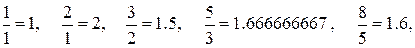
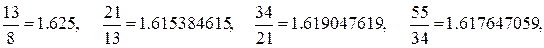
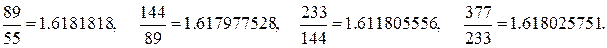
Ми бачимо, що відношення|ставлення| цих чисел коливається|вагається| біля|близько| значення 1.618 (якщо ігнорувати декілька перших значень). Цією властивістю числа Фібоначчі нагадують члени геометричної прогресії. Приймемо  (
(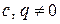 ). Тоді вираз|вираження|
). Тоді вираз|вираження|
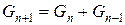
перетвориться в
 ,
,
який після|потім| спрощень виглядає так
 .
.
Ми одержали|отримали| квадратне рівняння, коріння якого рівне:
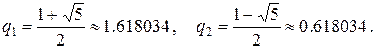
Тепер можемо записати:
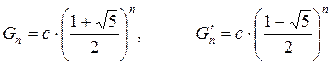
(де с|із| є|з'являється,являється| константою). Обидва члени 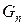 і
і 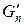 не дають чисел Фібоначчі, наприклад
не дають чисел Фібоначчі, наприклад  , тоді як
, тоді як  . Проте|однак| різниця
. Проте|однак| різниця  задовольняє рекурентному рівнянню:
задовольняє рекурентному рівнянню:
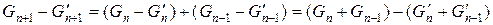 .
.
Для n=0 ця різниця дає 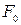 , тобто|цебто|:
, тобто|цебто|:  . Проте|однак| при n=1 ми маємо
. Проте|однак| при n=1 ми маємо  . Щоб одержати
. Щоб одержати  |отримати|, необхідно прийняти:
|отримати|, необхідно прийняти: 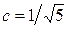 .
.
Тепер ми маємо дві послідовності:  і
і  , які починаються з однакових двох чисел і задовольняють одній і тій же рекурентній формулі. Вони повинні бути рівні:
, які починаються з однакових двох чисел і задовольняють одній і тій же рекурентній формулі. Вони повинні бути рівні: 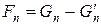 . Теорема доведена.
. Теорема доведена.
При зростанні n член 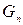 стає дуже великим, тоді як
стає дуже великим, тоді як 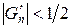 , і роль члена
, і роль члена 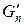 в різниці скорочується. Тому при великих n приблизно можемо записати
в різниці скорочується. Тому при великих n приблизно можемо записати
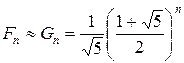 .
.
Ми ігноруємо 1/2 (оскільки числа Фібоначчі зростають до безкінечності при зростанні|зрості| n до безкінечності).
Відношення|ставлення| 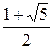 називається золотим перетином, його використовують за межами математики (наприклад, в архітектурі). Золотим перетином є|з'являється,являється| відношення|ставлення| між діагоналлю і стороною правильного п'ятикутника.
називається золотим перетином, його використовують за межами математики (наприклад, в архітектурі). Золотим перетином є|з'являється,являється| відношення|ставлення| між діагоналлю і стороною правильного п'ятикутника.
Читайте також:
- N – чисельність популяції
- Абсолютні й відносні посилання у формулах
- Аксіома неперервності дійсних чисел
- Алгоритми переведення чисел з однієї позиційної системи числення в іншу
- Аналіз чисельності, складу і руху персоналу
- Барометрична формула
- Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
- Введення чисел.
- Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
- Визначення суми на множині цілих невід’ємних чисел, її існування та єдиність. Операція додавання та її основні властивості (закони).
- Визначення чисельності окремих категорій працівників
- Визначення чисельності окремих категорій працівників
| <== попередня сторінка | | | наступна сторінка ==> |
| Сума чисел Фібоначчі | | | Прості числа |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |