• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Прості числа

Всі натуральні числа, великі одиниці, розпадаються на два класи. До першого відносяться числа, що мають рівно два натуральних дільника, одиницю і самого себе, до другого – всі інші. Числа першого класу називають простими, а другого – складними|складовими|. Прості числа в межах перших трьох десятків: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 .

Властивості простих чисел і їх зв'язок зо|із| всіма натуральними числами вивчалася Евклідом (3 вік|повік| до нашої ери). Якщо виписувати прості числа підряд, то можна відмітити|помітити|, що відносна щільність їх убуває. На перший десяток їх доводиться|припадає,приходиться| 4, тобто 40%, на сотню – 25, тобто 25%, на тисячу – 168, тобто менше 17%, на мільйон – 78498, тобто менше 8%, і т.д.. Проте|тим не менше|, їх загальне|спільне| число нескінченно.

Серед простих чисел попадаються|трапляються| пари таких, різниця між якими рівна двом (так звані прості близнята), проте|однак| кінцівка|скінченність| або нескінченність таких пар не доведена.

Евклід вважав|лічив| очевидним, що за допомогою множення тільки|лише| простих чисел можна одержати|отримати| всі натуральні числа, причому кожне натуральне число уявно у вигляді твору|добутку| простих чисел єдиним чином (з точністю до|із точністю до| порядку|ладу| множників). Таким чином, прості числа утворюють мультиплікативний базис натурального ряду|лави,низки|.

Вивчення розподілу простих чисел привело до створення|створіння| алгоритму, що дозволяє одержувати|отримувати| таблиці простих чисел. Таким алгоритмом є|з'являється,являється| решето Ератосфену (3 вік|повік| до нашої ери). Цей метод полягає у відсіюванні (наприклад, шляхом закреслення) тих цілих чисел заданої послідовності, які діляться хоч би на одне з простих чисел, менших .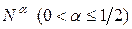

Теорема 6.2. (теорема Евкліда). Число простих чисел нескінченно.

Доказ. Теорему Евкліда про нескінченність числа простих чисел доведемо способом, запропонованим Леонардом Ейлером| (1707–1783). Ейлер розглянув|розгледів| добич|добуток| по всіх простих числах p:

при 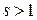. Ця добич|добуток| сходиться, і якщо її розкрити, то через однозначність розкладання натуральних чисел на прості співмножники виходить, що воно дорівнює сумі ряду 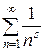|лави,низки|, звідки слідує|прямує| тотожність Ейлера:

.

Оскільки|тому що| при 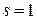ряд|лава,низка| справа розходиться (гармонійний ряд|лава,низка|), то з|із| тотожності Ейлера виходить теорема Евкліда.

Російський математик П.Л. Чебишев (1821–1894) вивів формулу, що визначає межі, в яких поміщено|ув'язнено| число простих чисел , що не перевершують X:

,

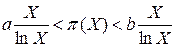де .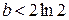

Читайте також:

1. Абсолютна величина числа позначається символом .
2. Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
3. Арифметичні операції над цілими числами
4. Бухгалтерські записи (проводки) – прості та складні.
5. Визначення числа одиниць переносу
6. Визначення числа прокладок
7. Визначення. Числа й називаються комплексно спряженими.
8. Вимірний арифметичний простір
9. Власні і загальні іменники як лексико-граматичні розряди за специфікою виявлення категорії числа
10. Власні числа та власні вектори матриці
11. Внутрішній простір будівель
12. Воднеподібні атоми в квантовій механіці. Квантові числа

Переглядів: 832