• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

РОЗДІЛ 7. МАТЕМАТИЧНА ОБРОБКА РЕЗУЛЬТАТІВ ВИМІРІВ

§ 1. Математична обробка ряду рівноточних вимірів

Математична обробка ряду рівноточних вимірів полягає в послідовному визначенні числових характеристик вимірюваної величини (§ 3, розд.6).

Для зручності приведемо послідовність обчислень при обробці ряду рівноточних вимірів. Припустимо, що в результаті повторних рівноточних вимірів величини Х отримано ряд результатів

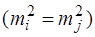(7.1)

Обчислюють

1. Просту арифметичну середину за формулою

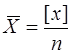. (7.2)

Для зручності обчислень можна взяти умовне значення близьке до виміряних результатів х₀. Обчислити різниці

, .

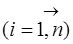Тоді 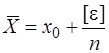. (7.3)

2. При відомому істинному значенні Х обчислюють величину систематичної похибки lза формулою

. (7.4)

3. Абсолютні похибки вимірів при заданому істинному значенні Х

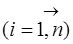, , (7.5)

або ймовірні похибки, коли невідоме істинне значення вимірюваної величини Х

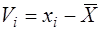, (7.6)

Контроль [V_i] = 0 – в межах точності обчислень.

4. Величини [pD²] або [pV²] з контролем

Контроль

. (7.7)

5. Середню квадратичну похибку окремого виміру :

а) за формулою Гаусса

; (7.8)

б) або за формулою Бесселя

. (7.9)

6. Середню квадратичну похибку середнього арифметичного

. (7.10)

Далі обчислюють оцінки надійності і середніх квадратичних похибок m i M.

7. Середню квадратичну похибку середньої квадратичної похибки

. (7.11)

При цьому m ³ t_b m_m. Параметр t визначається за таблицями розподілу Стьюдента (дод. 3) залежно від заданої ймовірності bта числа ступенів вільності п.

8. Середню квадратичну похибку середньої квадратичної похибки арифметичного середнього

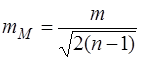. (7.12)

Надійність визначення СКП арифметичного середнього М контролюють нерівністю

М ³ t_b m_М.

9. Визначають довірчі інтервали для:

а) можливого значення істинної величини

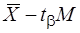
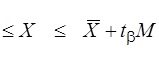, (7.13)

де t_b – параметр вибирається із таблиць розподілу Стьюдента (дод. 3) залежно від заданої ймовірності bта кількості ступенів вільності k = п – 1;

б) можливих значень результатів вимірів

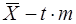
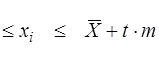, (7.14)

де параметр t вибирається так само, як і в попередньому випадку.

Якщо в ряду вимірів є результати, що виходять за межі визначеного параметра, то їх або повторюють, або виміри виключають і попередні обчислення виконують повторно;

в) дисперсії та стандарти середнього арифметичного

; (7.15)

. (7.16)

г) стандарту окремих вимірів

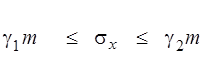, (7.17)

де m і M – середні квадратичні похибки, обчислені за формулами (7.7, 7.8 та 7.9).

Коефіцієнти g₁ і g₂ обчислюються за формулами

, – (7.18)

при використані формули (7.8),

або 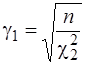, 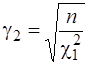– (7.19)

при використанні формули (7.7),

статистики і 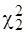вибираються із таблиць розподілу Пірсона (дод.4) за числом ступенів вільності (п – 1) або п та заданій імовірності b при

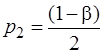і р₁ = 1 – р₂. (7.20)

Приклад. При створенні польового компаратора його довжина виміряна еталонним дротом 12 разів (табл.7.1). Виконати обробку ряду рівноточних вимірів. Надійність оцінок точності визначити при ймовірності b = 0,95.

Розв’язання. Результати вимірів і обчислень зведемо до табл. 7.1.

Таблиця 7.1

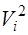
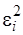
№ пор.	Li м	eі мм	Vi мм			Контрольні обчислення
	120.012		+2.9	8.4
	120.005		-4.1	16.8		[V2] = - 0.2
	120.009		-0.1
	120.001		-8.1	65.6		[V2] = [x2]-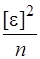
	120.015		+5.9	34.8		216 = 1207 – 11881/12 = = 218
	120.008		-1.1	1.2
	120.010		+0.9	0.8
	120.013		+3.9	15.2	16.9
	120.015		+5.9	34.8
	120.004		-5.1	26.0
	120.006		-3.1	9.6
	120.011		+1.9	3.6
L0	120.000		+21.4	216.0
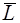
	120.0091	-21.6
		[V] = - 0.2

За формулами (7.2) – (7.17) обчислюємо:

Читайте також:

1. II. Обробка результатів
2. III. Економічна інтерпретація результатів статистичного дослідження банків
3. IV розділ. Сегментація ринку та вибір цільового сегменту
4. IІI розділ. Аналіз стану маркетингового середовища підприємства
5. V розділ. Товарна політика підприємства
6. VI розділ. Маркетингова цінова політика
7. VII розділ. Маркетингові рішення з розподілу та збуту товару
8. VIII розділ. Маркетингова політика комунікацій
9. А) Роздільне складання таблиць (За підручником Богдановича М.В.)
10. Абсолютні та відності показники результатів діяльності підприємства.
11. Аварійно-рятувальні підрозділи Оперативно-рятувальної служби цивільного захисту, їх призначення і склад.
12. Актив і пасив балансу складаються також з певних розділів.

Переглядів: 648