• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ряди вимірів будуть рівноточними, коли

Q £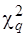, (5.29)

де 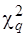визначають за таблицями дод.9із рівня значності q і числа ступенів вільності k = п – 1.

Якщо S_i = S_j, а N = n × S , то можна обчислити статистику Q_i за формулою

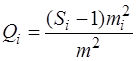. (5.30)

При цьому 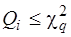. 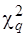визначають за аргументами q та k = S – 1(дод. 9).

Приклад 6. Дослідження осідання греблі виконано по 4-х реперах. Всього виконано 6 циклів спостережень. Із обробки рядів вимірів отримано дисперсії: 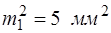; ; 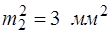; 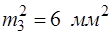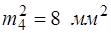. Визначити рівноточність рядів вимірів при ймовірності р = 0,99.

Розв’язання. За формулою (5.25) обчислюємо незміщену оцінку дисперсії матриці виміряних величин. При S_i = S_j = 6та n = 4, N = 24, 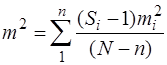= 33,5 мм². Обчислюємо за формулою (5.27) значення С = 1,08 та статистику Q за формулою (5.26 ), отримаємо Q = 4,45. Із таблиці дод. 9 при q = 0,01 та k = п – 1 = 3, 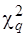=11,3.Оскільки |Q| < 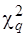(4,45 < 11,3), то ряди вимірів є рівноточними. До такого висновку прийдемо, коли використаємо формулу (5.30), так як S_i = S_j = 6.

§ 2. Перевірка закону розподілу статистичних рядів

Важливе значення при математичній обробці геодезичних вимірів має знання закону розподілу результатів або похибок вимірів. Найкращі оцінки отримують, коли ряд вимірів підпорядковується нормальному закону розподілу. Однак, практично комплекс умов постійно дещо змінюється. В наслідок цього виникає відхилення закону розподілу результатів вимірів від теоретичного значення функцій розподілу.

Практично на основі тих чи інших відомостей висувають припущення або (“нульову”) гіпотезу про вид закону розподілу статистичного ряду, створеного за результатами вимірів. Шляхом застосування різних критеріїв перевірки визначають, чи є допустимим розходження між дослідним і теоретичним (передбачуваним) законом розподілу.

Враховуючи, що результати геодезичних вимірів, як правило, підпорядковуються нормальному закону розподілу при дотриманні “комплексу умов” або вимог нормативно-технічної документації, розглянемо ряд критеріїв перевірки відповідності нормальному закону розподілурезультатів вимірів:

1. Перевірка по асиметрії і ексцесу

Гіпотезу про нормальний закон розподілу статистичного ряду називають нульовою або основною. Маємо статистичний ряд х₁, х₂, ..., х_п і висунута гіпотеза, що він підпорядковується нормальному закону розподілу (НЗР). За формулами § 4 можна визначити числові характеристики НЗР: математичне сподівання або середнє арифметичне, дисперсію, середню квадратичну похибку, асиметрію S_k та ексцес E_k.

Скористаємося тим, що асиметрія S_k (4.41) та ексцес Е_k (4.42) є числовими характеристиками, що характеризують ступінь відхилення досліджуваного розподілу від теоретичного НЗР. Вони, як і інші параметри НЗР є випадковими величинами, а тому можуть відхилятися від нуля.

Мірою точності асиметрії та ексцесу є дисперсії

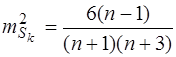; (5.31)

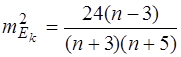. (5.32)

Читайте також:

1. Будуть тебе шанувати.
2. Довірчий інтервал характеризує точність вимірів даної вибірки, а довірча імовірність – достовірність виміру.
3. За даного розподілу владних повноважень районні державні адміністрацій будуть ліквідовані.
4. Звісно ж, це забезпечує величезні можливості людського самопізнання, осягнення таких суто людських вимірів буття, як спілкування, моральність, творчість тощо.
5. Квантові межі точності вимірів
6. Контрольні роботи, які представлені без дотримання зазначених правил, а також роботи, виконані не за своїм варіантом, зараховуватись не будуть.
7. Метрологічне забезпечення вимірів апаратурою АК
8. Метрологічне забезпечення вимірів апаратурою гамма-гамма каротажу
9. Метрологічне забезпечення вимірів апаратурою нейтронних методів
10. Метрологічне забезпечення вимірів апаратурою термокаротажу
11. На малюнку зображена модель монополістичної конкуренції. Який обсяг і по якій ціні будуть пропонувати фірми на ринку монополістичної конкуренції?
12. Нарахування амортизації не спричиняють грошових витрат. Якщо не враховувати знос, то витрати будуть занижені, а прибуток та податок на прибуток будуть завищені.

Переглядів: 503