
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Варіанти для самостійного розв’язання
Варіант 1
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідну 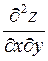 функції
функції  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції 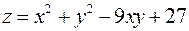 в замкненій області
в замкненій області  :
: 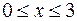 ,
, 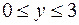 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці 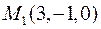 та похідну в точці
та похідну в точці  у напрямі вектора
у напрямі вектора 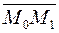 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 4,3 | 5,3 | 3,8 | 1,8 | 2,3 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 2
1. Знайти та відобразити на рисунку область визначення функції 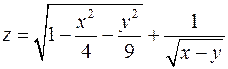 .
.
2. Знайти похідну 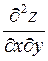 функції
функції 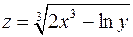 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці 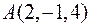 .
.
4. Знайти найменше та найбільше значення функції 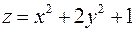 в замкненій області
в замкненій області  :
: 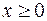 ,
, 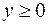 ,
, 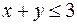 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 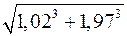 .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці 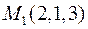 та похідну в точці
та похідну в точці 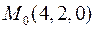 у напрямі вектора
у напрямі вектора 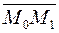 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 4,5 | 5,5 | 4,0 | 2,0 | 2,5 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 3
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідну 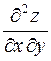 функції
функції  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 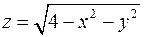 в точці
в точці 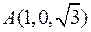 .
.
4. Знайти найменше та найбільше значення функції 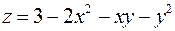 в замкненій області
в замкненій області  :
:  ,
, 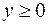 ,
,  .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції 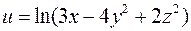 знайти градієнт в точці
знайти градієнт в точці 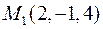 та похідну в точці
та похідну в точці 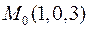 у напрямі вектора
у напрямі вектора 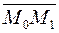 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 4,7 | 5,7 | 4,2 | 2,2 | 2,7 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 4
1. Знайти та відобразити на рисунку область визначення функції 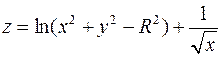 .
.
2. Знайти похідну 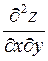 функції
функції  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 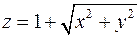 в точці
в точці 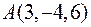 .
.
4. Знайти найменше та найбільше значення функції  в замкненій області
в замкненій області  :
: 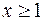 ,
, 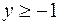 ,
, 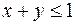 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції 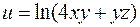 знайти градієнт в точці
знайти градієнт в точці  та похідну в точці
та похідну в точці  у напрямі вектора
у напрямі вектора 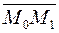 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 4,9 | 5,9 | 4,4 | 2,4 | 2,9 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 5
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідну 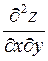 функції
функції 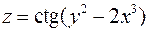 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 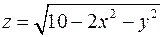 в точці
в точці 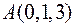 .
.
4. Знайти найменше та найбільше значення функції 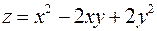 в замкненій області
в замкненій області  :
: 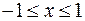 ,
,  .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції 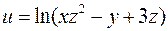 знайти градієнт в точці
знайти градієнт в точці 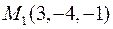 та похідну в точці
та похідну в точці  у напрямі вектора
у напрямі вектора 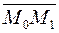 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 5,1 | 6,1 | 4,6 | 2,6 | 3,1 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 6
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідну 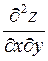 функції
функції  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 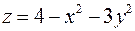 в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції  в замкненій області
в замкненій області  :
: 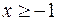 ,
, 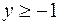 ,
, 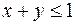 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції 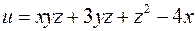 знайти градієнт в точці
знайти градієнт в точці 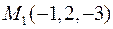 та похідну в точці
та похідну в точці 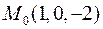 у напрямі вектора
у напрямі вектора 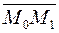 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 3,9 | 4,9 | 3,4 | 1,4 | 1,9 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 7
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідну 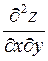 функції
функції 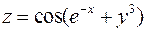 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці 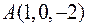 .
.
4. Знайти найменше та найбільше значення функції 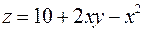 в замкненій області
в замкненій області  :
: 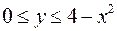 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції 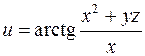 знайти градієнт в точці
знайти градієнт в точці  та похідну в точці
та похідну в точці 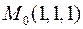 у напрямі вектора
у напрямі вектора 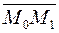 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 5,2 | 6,2 | 4,7 | 2,7 | 3,2 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 8
1. Знайти область існування функції  .
.
2. Знайти похідну 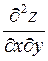 функції
функції 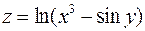 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 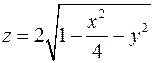 в точці
в точці 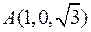 .
.
4. Знайти найменше та найбільше значення функції 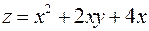 в замкненій області
в замкненій області  :
:  ,
, 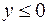 ,
,  .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 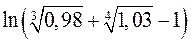 .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці 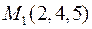 та похідну в точці
та похідну в точці 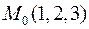 у напрямі вектора
у напрямі вектора 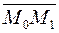 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 5,5 | 6,5 | 5,0 | 3,0 | 3,5 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 9
1. Знайти та відобразити на рисунку область визначення функції 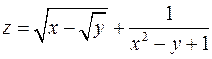 .
.
2. Знайти похідну 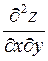 функції
функції  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 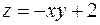 в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції 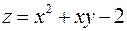 в замкненій області
в замкненій області  :
:  .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 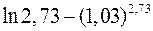 .
.
6. Для функції 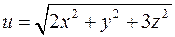 знайти градієнт в точці
знайти градієнт в точці  та похідну в точці
та похідну в точці  у напрямі вектора
у напрямі вектора 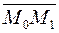 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 5,7 | 6,7 | 5,2 | 3,2 | 3,7 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 10
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідну 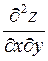 функції
функції 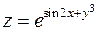 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 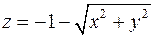 в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції 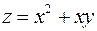 в замкненій області
в замкненій області  :
: 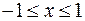 ;
; 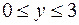
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 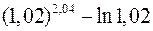 .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці 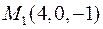 та похідну в точці
та похідну в точці  у напрямі вектора
у напрямі вектора 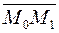 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 5,9 | 6,9 | 5,4 | 3,4 | 3,9 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 11
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідну 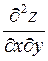 функції
функції 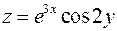 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 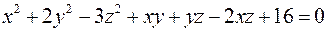 в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції  в замкненій області
в замкненій області  :
: 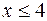 ;
; 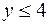 ;
; 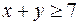 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 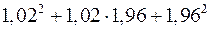 .
.
6. Для функції 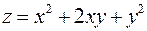 знайти градієнт в точці
знайти градієнт в точці 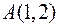 та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора  .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 5,3 | 6,3 | 4,8 | 2,8 | 3,3 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 12
1. Знайти та відобразити на рисунку область існування функції 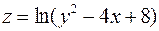 .
.
2. Знайти похідні другого порядку від функції 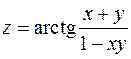 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 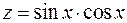 в точці
в точці 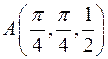 .
.
4. Знайти найменше та найбільше значення функції  в області
в області  :
: 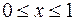 ;
; 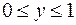 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 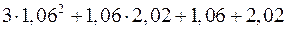 .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці 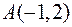 та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора  .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 3,3 | 4,3 | 2,8 | 0,8 | 1,4 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 13
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідні другого порядку від функції 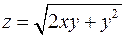 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції  в замкненій області
в замкненій області  :
: 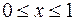 ;
; 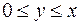 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 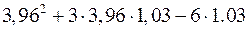 .
.
6. Для функції 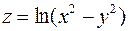 знайти градієнт в точці
знайти градієнт в точці 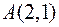 та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора  .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 6,3 | 7,2 | 5,9 | 3,8 | 4,2 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 14
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідні другого порядку від функції 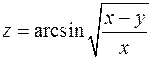 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 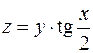 в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції  в замкненій області
в замкненій області  :
:  ;
; 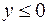 ;
;  .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції 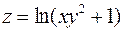 знайти градієнт в точці
знайти градієнт в точці  та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора 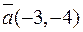 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 2,9 | 3,8 | 2,4 | 0,5 | 0,8 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 15
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Знайти похідні другого порядку від функції  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 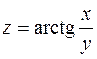 в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції 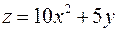 в замкненій області
в замкненій області  :
: 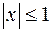 ;
;  .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 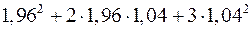 .
.
6. Для функції 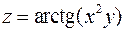 знайти градієнт в точці
знайти градієнт в точці 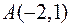 та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора 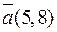 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 1,8 | 1,4 | 3,3 | 4,8 | 3,9 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 16
1. Знайти та відобразити на рисунку область визначення функції 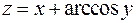 .
.
2. Знайти похідні другого порядку від функції 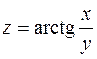 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції 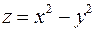 в замкненій області
в замкненій області  :
: 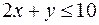 ;
; 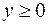 ;
;  .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції 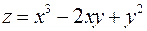 знайти градієнт в точці
знайти градієнт в точці  та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора  .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 3,1 | 2,4 | 4,2 | 5,5 | 4,4 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 17
1. Знайти та відобразити на рисунку область визначення функції 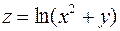 .
.
2. Знайти похідні другого порядку від функції  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції 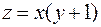 в замкненій області
в замкненій області  :
:  ;
; 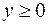 ;
; 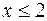 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції 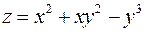 знайти градієнт в точці
знайти градієнт в точці 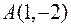 та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора 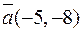 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 2,3 | 2,0 | 4,2 | 5,8 | 5,2 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 18
1. Знайти та відобразити на рисунку область визначення функції 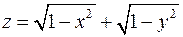 .
.
2. Знайти похідні другого порядку від функції 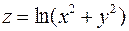 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції 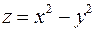 в замкненій області
в замкненій області  :
: 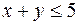 ;
; 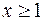 ;
; 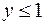 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 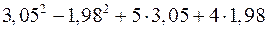 .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці  та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора 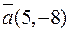 .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 4,5 | 5,7 | 4,4 | 2,6 | 1,9 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 19
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Показати, що функція 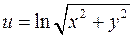 задовольняє рівнянню Лапласа
задовольняє рівнянню Лапласа 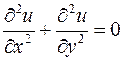 .
.
3. Скласти рівняння дотичної площини і нормалі до поверхні  в точці
в точці  .
.
4. Знайти найменше та найбільше значення функції 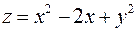 в області
в області  :
: 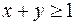 ;
;  ;
; 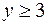 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці 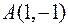 та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора  .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 4,7 | 5,9 | 4,6 | 1,8 | 2,2 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 20
1. Знайти та відобразити на рисунку область визначення функції 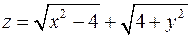 .
.
2. Показати, що функція 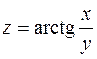
 задовольняє рівнянню Лапласа
задовольняє рівнянню Лапласа 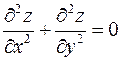 .
.
3. Скласти рівняння дотичної площини і нормалі до поверхні  в точці
в точці 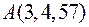 .
.
4. Знайти найменше та найбільше значення функції 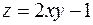 в області
в області  :
: 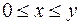 ;
; 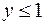 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 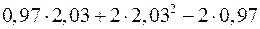 .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці  та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора  .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 5,1 | 5,9 | 4,2 | 2,0 | 2,3 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 21
1. Знайти та відобразити на рисунку область визначення функції 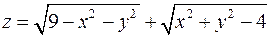 .
.
2. Показати, що функція  , де
, де 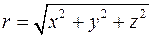 , а
, а  , задовольняє рівняння Гельмгольца
, задовольняє рівняння Гельмгольца  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 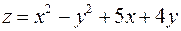 в точці
в точці  .
.
4. Виготовити з картону прямокутну коробку (без кришки) ємності  з найменшими витратами матеріалу.
з найменшими витратами матеріалу.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 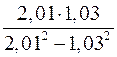 .
.
6. Знайти похідну функції 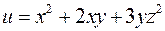 в точці
в точці 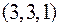 у напрямі градієнта цієї функції.
у напрямі градієнта цієї функції.
7. Експериментально одержано значення функції  :
:

| |||||

| 3,2 | 2,4 | 4,6 | 5,9 | 4,8 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 22
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Показати, що функція 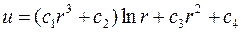 , де
, де  , а
, а 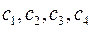 – довільні сталі, задовольняє рівняння Максвелла
– довільні сталі, задовольняє рівняння Максвелла 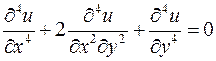 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 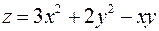 в точці
в точці 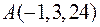 .
.
4. В кулю діаметру 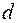 вписати прямокутний паралелепіпед найбільшого об’єму.
вписати прямокутний паралелепіпед найбільшого об’єму.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити 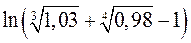 .
.
6. Знайти похідну функції 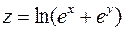 в точці
в точці 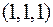 у напрямі градієнта цієї функції.
у напрямі градієнта цієї функції.
7. Експериментально одержано значення функції  :
:

| |||||

| 3,7 | 3,2 | 5,2 | 6,7 | 5,8 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 23
1. Знайти та відобразити на рисунку область визначення функції 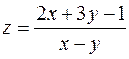 .
.
2. Показати, що функція  задовольняє рівняння
задовольняє рівняння 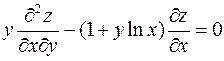 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні 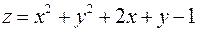 в точці
в точці  .
.
4. Знайти розміри циліндричної посудини найбільшої місткості з поверхнею  .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Знайти градієнт функції  в точці
в точці 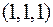 та похідну в цій точці у напрямі градієнта.
та похідну в цій точці у напрямі градієнта.
7. Експериментально одержано значення функції  :
:

| |||||

| 3,5 | 3,0 | 5,0 | 6,5 | 5,6 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 24
1. Знайти та відобразити на рисунку область визначення функції  .
.
2. Показати, що функція  задовольняє рівнянню
задовольняє рівнянню  .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці 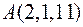 .
.
4. Поверхня прямокутного паралелепіпеда дорівнює 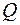 . Знайдіть розмір паралелепіпеда найбільшого об’єму.
. Знайдіть розмір паралелепіпеда найбільшого об’єму.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Знайти градієнт функції  в точці
в точці  та похідну в цій точці у напрямі вектора
та похідну в цій точці у напрямі вектора  .
.
7. Експериментально одержано значення функції  :
:

| |||||

| 2,9 | 2,4 | 4,5 | 5,8 | 4,9 |
Методом найменших квадратів знайти функцію  , яка виражає наближено (апроксимує) функцію
, яка виражає наближено (апроксимує) функцію  . Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції
. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції  .
.
Варіант 25
1. Знайти та відобразити на рисунку область визначення функції 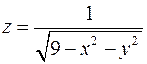 .
.
2. Показати, що функція  задовольняє рівняння
задовольняє рівняння 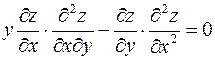 .
.
3. Знайти рівняння дотичної площини і нормалі до поверхні  в точці
в точці 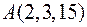 .
.
4. Знайти прямокутний паралелепіпед найбільшого об’єму за умови, що довжина його діагоналі дорівнює 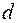 .
.
5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити  .
.
6. Для функції  знайти градієнт в точці
знайти градієнт в точці 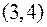 та похідну в цій точці у напрямі градієнта.
та похідну в цій точці у напрямі градієнта.
7. Експериментально одержано значення функції  :
:

| |||||

| 1,9 | 2,4 | 4,4 | 5,7 | 4,6 |
Ме
Читайте також:
- IV. Перевірка розв’язання і відповідь
- Актуальні проблеми регіональної політики та їх розв’язання.
- Алгоритм розв’язання
- Алгоритм розв’язання
- Алгоритм розв’язання задачі
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- АЛОМОРФИ І ВАРІАНТИ МОРФЕМ
- Альтернативні варіанти виробництва при повній зайнятості ресурсів
- Альтернативні варіанти геополітичної орієнтації України
- Альтернативні варіанти довгострокового фінансування діяльності підприємства
- Аналіз причин виникнення проблеми та обґрунтування її розв’язання програмним методом
| <== попередня сторінка | | | наступна сторінка ==> |
| Метод найменших квадратів | | | RAMBLER.RU |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |