• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Момент сил пари та момент пари сил

Теорема. Сума моментів сил пари відносно довільного центра в просторі є величиною сталою для даної пари і називається векторним моментом цієї пари.

Доведення. Нехай задано пару сил ( 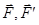), плече якої AB=h (рис. 4.2). Оскільки дія пари на тіло характеризується обертальним ефектом, знайдемо суму моментів сил пари відносно центра О, довільно розміщеного в просторі. Одержимо:

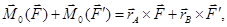(4.2)

де 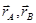- радіуси-вектори точок прикладання сил і 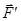відносно центра О. З урахуванням формул (4.1) рівність (4.2) запишеться так:

(4.3)

Тут 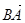- радіус-вектор точки А , у якій прикладено силу пари, відносно центра В , а тому 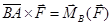. Отже,

(4.4)

Відомо, що вектор перпендикулярний до площини векторів ВА і , а його модуль

. (4.5)

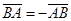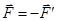Аналогічно, врахувавши що і , одержимо

де вектор 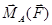перпендикулярний до площини векторів і , а,

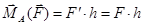. (4.6)

Отже, доведено, що сума моментів сил пари відносно довільного центра в просторі не залежіть від вибору цього центра і дорівнює моменту однієї із сил пари відносно точки прикладання іншої сили.

Ця сума моментів характеризує обертальну дію пари сил на тіло і назвемо її моментом пари сил. Позначимо момент пари сил , або просто . Отже,

. (4.7)

Теорему доведено.

З доведення теореми випливає, що момент пари сил є вектором. Визначимо його величину і напрямок.

Читайте також:

1. I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ
2. II. Організаційний момент.
3. M – моменты
4. Алгебраїчний момент пари сил
5. Аналітичний вираз сил і моментів.
6. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
7. Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
8. В положение ее в данной момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется переменками.
9. В соответствии со ст.412.13 УПК РФ Постановление Президиума Верховного Суда Российской Федерации вступает в законную силу с момента его провозглашения.
10. Величина і напрямок векторного момента пари сил
11. Вибір моменту для відкриття вогню
12. Визначення балансової вартості валюти в момент її вибуття.

Переглядів: 718