• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поняття розбиття множини на підмножини, що попарно не перетинаються. Класифікація понять. Приклади класифікацій

Суть будь-якої класифікації (понять, відношень і т.ін.) зводиться до того, що елементи однієї (універсальної) множини за певними характеристичними ознаками розбиваються на дві або кілька непорожніх підмножин так, щоб кожен елемент даної множини входив в одну і тільки одну з підмножин, тобто щоб ці підмножини попарно не перетинались, інакше, щоб переріз кожної пари з них був порожньою множиною.

Яскравим прикладом класифікації понять є класифікація чисел: множина комплексних чисел поділяється на дві підмножини, що не перетинаються, - множину дійсних чисел і множину уявних чисел. Множина дійсних чисел поділяється на дві підмножини, що не перетинаються, - множину раціональних і множину ірраціональних чисел.

Нехай універсальною множиною є множина натуральних чисел. Візьмемо за основу класифікації властивість, пов’язану з кількістю дільників числа. Тоді множину натуральних чисел розбивають на три підмножини, що попарно не перетинаються:

1) множину натуральних чисел, які мають тільки два дільники: одиницю і самі себе – прості числа Р 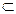N;

2) множину натуральних чисел, які мають більше двох дільників (крім 1 і самого себе мають ще якийсь дільник) – складені числа С 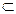N;

3) одноелементну множину {1}. Число 1 не належить ні до простих чисел, ні до складених, бо має лише один дільник – само себе {1} 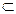N.

Ці три підмножини попарно не перетинаються.

Розглянемо ще приклад класифікації геометричних понять. Нехай універсальною множиною є множина трикутників А. Залежно від рівності сторін множину трикутників поділяють на дві підмножини, перерізом яких є порожня множина: множина В трикутників, у яких є принаймні по дві рівні сторони – рівнобедрені трикутники; множина С різносторонніх трикутників. В свою чергу. Множина В рівнобедрених трикутників поділяється на дві підмножини, що не перетинаються: множина трикутників, у яких тільки дві сторони рівні, це рівнобедрені, але не рівносторонні; множина К трикутників, у яких всі три сторони рівні – рівносторонні.

Для того щоб не допустити при класифікації помилок, які призводять до неправильного розв’язання задач, зокрема рівнянь та нерівностей, слід пам’ятати дві умови:

1) підмножини (жодна пара їх), на які розбиваємо основну множину, не повинні мати спільних елементів, тобто множини їх попарних перерізів повинні бути порожніми: А_i ∩ A_j = ø , і ≠ j;

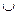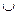2) класифікація повинна бути повною, вичерпною. Це означає, що жоден елемент основної множини не повинен залишитись не охопленим однією з множин: А₁ А₂ А₃ 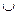… 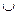А_k = U

Кількість елементів універсальної множини при розбитті її на підмножини повинна дорівнювати сумі кількостей елементів усіх підмножин:

n(U) = n(A₁) + n(A₂) + … + n(A_k)

Так, наприклад, не можна класифікувати функції на парні і непарні, як це роблять часто учні за аналогією з поділом натуральних чисел, бо окрім парних і непарних функцій є ще функції, які не належать ні до парних, ні до непарних.

Читайте також:

1. II. Класифікація видатків та кредитування бюджету.
2. II. Поняття соціального процесу.
3. V. Класифікація і внесення поправок
4. V. Класифікація рахунків
5. V. Поняття та ознаки (характеристики) злочинності
6. VII. Поняття про рану, рановий процес, види загоювання ран
7. А. Структурно-функціональна класифікація нирок залежно від ступеню злиття окремих нирочок у компактний орган.
8. А/. Поняття про судовий процес.
9. Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
10. Адміністративний проступок: поняття, ознаки, види.
11. Адміністративні провадження: поняття, класифікація, стадії
12. Акти застосування юридичних норм: поняття, ознаки, види.

Переглядів: 5599