• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Дроби та їх властивості

Означення. Символ , де т і п натуральні числа, називають дробом, т – чисельник дробу і п – знаменник.

Дріб означає, що одна п-на частина одиниці виміру е міститься т разів у відрізку а, тобто одиничний відрізок розділили на п рівних частин і взяти т таких частин. Це записується так: а = е,

Дріб є мірою довжини відрізка а при одиниці довжини е.

Повернемось до випадку 2) а = 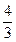е, це не єдиний розв’язок, бо якщо поділимо е на 6 рівних частин, то отримаємо а = 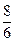е і т.д.

Тобто, довжина відрізка а може бути виражена нескінченною множиною дробів: , , , …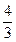

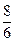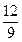Означення. Дроби, які виражають довжину одного і того ж відрізка при одиниці довжини е, називаються рівними.

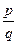Якщо дроби і рівні, то записують = .

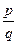Необхідна і достатня умова рівності дробів

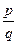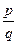
Два дроби і рівні тоді і тільки тоді, коли виконується умова mq=np, тобто = mq=np

Доведення.

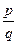
а) Доведемо, що = mq=np

Для будь-якого натурального числа q = 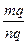, а для будь-якого натурального числа п 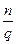= 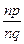. Тоді з рівності дробів і 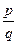випливає 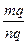= 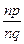. Оскільки знаменники цих дробів рівні, то і чисельники їх будуть рівні: mq=np.

б) Доведемо тепер, навпаки, що mq=np 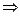= 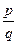. Розділимо обидві частини mq=np на натуральне число nq, тоді отримаємо . Але 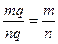, 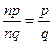. Тоді, = .

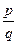Рівні дроби вважають різними записами одного і того ж числа, а саме число називають додатним раціональним числом.

Дріб – це лише форма зображення числа. Дробове число 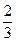можна зобразити (записати) різними рівними дробами: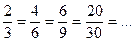

Дроби 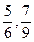, … зображають зовсім інші числа: і ін.

Для будь-якого додатного раціонального числа існує один і тільки один нескоротний дріб, що є записом цього числа.

Множина додатних раціональних чисел – це множина натуральних чисел в об’єднанні з множиною дробових чисел. Множину додатних раціональних чисел позначають Q₊. Множина натуральних чисел є підмножиною множини додатних чисел, тобто N 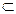Q₊.

Дріб, чисельник якого менший від знаменника, називається правильним; дріб, чисельник якого більший або дорівнює знаменнику, називається неправильним. Наприклад, 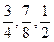– правильні; 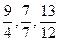– неправильні дроби.

Дріб , чисельник і знаменник якого є числа взаємно прості, тобто D(т;п)=1, називається нескоротним дробом.

Основна властивість дробу: Якщо чисельник і знаменник дробу помножити на те саме натуральне число, то дістанемо дріб, що дорівнює даному: , де k – натуральне число.

Застосування основної властивості дробу:

· скорочення дробів (заміна даного дробу іншим, що дорівнює йому, але з меншим чисельником і знаменником);

· зведення дробів до спільного знаменника (це заміна дробів рівними їм дробами, що мають однакові знаменники).

·

Наприклад.

1. Скоротити дріб .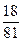

1-ий спосіб: чисельник і знаменник дробу ділити послідовно на спільні прості дільники: 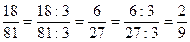, (2; 9) = 1

2-ий спосіб: знайти НСД чисельника і знаменника та поділити чисельник і знаменник відразу на їх НСД.

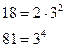
НСД (18; 81) = = 9

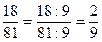, (2; 9) = 1.

2. Звести до найменшого спільного знаменника дроби:

а)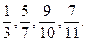

Знаменники цих дробів попарно взаємно прості. Тому НСК (3; 7; 10; 11) = =3 · 7 · 10 · 11 = 2310

Тоді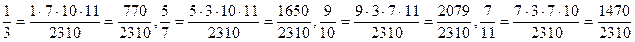

б)

64:8 і 64:32, тому НСК (8; 32; 64) = 64.

Тоді

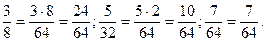
в)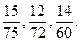

Маємо скоротні дроби, перед зведенням їх до найменшого спільного знаменника потрібно ці дроби скоротити.

Скоротимо ці дроби: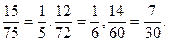

НСК (5; 6; 30) = 30

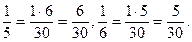
Отже,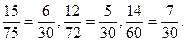

г) 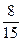і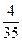

15 = 3 · 5, 35 = 5 · 7

НСК (15; 35) = 3 · 5 · 7 = 105.

Тоді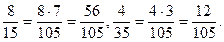

3. Побудувати відрізок, довжина якого виражена числом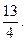

Побудова:

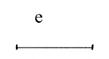1) обираємо одиницю довжини е

2) ділимо відрізок е на 4 рівні частини

3) відкладаємо на промені Ох 13 відрізків, кожний з яких дорівнює четвертій частині відрізка е.

Отримаємо відрізок ОА, довжина якого виражена числом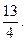

Поняття дробу вводять в початкових класах. За програмою з математики в 2 класі передбачено ознайомлення з частинами числа: половиною, третиною, чвертю, п’ятою частиною. В 3 класі учні розуміють сутність поняття частина числа; знаходять половину, третину, четверту на інші частини від числа, число за його частиною. В 4 класі розділ «Дроби». Тут за одиницю беруть відрізок, круг, прямокутник, зокрема квадрат, смужки та ін. 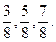Наприклад, круг ділять на 8 рівних частин і виділяють частину круга, Вводять поняття чисельника і знаменника дробу: число під рискою означає, на скільки рівних частин поділено ціле, його називають знаменником дробу. Число над рискою означає, скільки взято рівних частин. Це число називають чисельником дробу.

Учні записують і читають дроби; знаходять дріб від числа та число за його дробом; порівнюють дроби з однаковими знаменниками.

Читайте також:

1. OПТИЧНІ ВЛАСТИВОСТІ КОЛОЇДНИХ СИСТЕМ
2. А) Товар і його властивості.
3. Аеродинамічні властивості колісної машини
4. Алкани (насичені вуглеводні). Хімічні властивості алканів
5. Алкани, їх хімічні властивості.
6. Алкени. Хімічні властивості
7. Алкіни. Хімічні властивості
8. Аміни. Фізичні та хімічні властивості аліфатичних амінів.
9. Аналізатори людини та їхні властивості.
10. Аналізатори людини та їхні властивості.
11. АНТИДЕТОНАЦІЙНІ ВЛАСТИВОСТІ
12. Арифметичні дії над дійсними невід’ємними числами. Їхні властивості

Переглядів: 5128