
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Визначення арифметичних дій над додатними раціональними числами
Додавання невід’ємних раціональних чисел
1. Означення дії додавання дробових чисел. Нехай маємо два раціональних числа r1 і r2, виражені дробами з різними чисельниками і однаковими знаменниками:
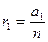 і
і 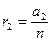
Їх можна розглядати як міри довжин двох відрізків b і с при одній одиниці вимірювання, або як числові характеристики множини 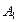 , що містить а1 n-хчасток деякого одиничного елемента, і множини
, що містить а1 n-хчасток деякого одиничного елемента, і множини  , що містить а2 таких самих n-х часток.
, що містить а2 таких самих n-х часток.
Додаючи ці два відрізки або об’єднуючи ці дві множини, дістаємо відрізок b+c або нову множину n-х часток деякого одиничного елемента. Ця нова множина буде містити 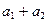 елементів, тобто n-х часток, отже, вона характеризуватиметься дробовим числом
елементів, тобто n-х часток, отже, вона характеризуватиметься дробовим числом 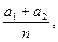 яке природно назвати сумою чисел
яке природно назвати сумою чисел  і
і 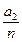 , тобто
, тобто 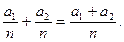
Аналогічні міркування можна провести і на випадок кількох, наприклад k, доданків.
Означення.Сумою двох (або кількох) дробових чисел з однаковими знаменниками є дробове число, чисельником якого є сума їх чисельників, а знаменником — їх спільний знаменник:

Означення.Сумою невід’ємних раціональних чисел  і
і 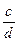 називається число
називається число 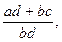 тобто:
тобто: 
Візьмемо два будь-які натуральні числа а і с та зобразимо їх у вигляді дробів із знаменниками 1, тоді, за означенням додаванні дробів, матимемо
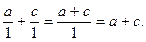
Зобразимо тепер а і с у вигляді дробів із знаменниками b і d і застосуємо правило додавання дробів з різними знаменниками:
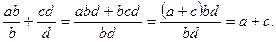
Звідси видно, що означення суми раціональних невід’ємних чисел є узагальненням означення суми натуральних чисел.
Наприклад. 5 + 3 = 8;
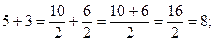

Мішані числа
Означення.Сума натурального і дробового чисел, записаних поряд без знака додавання, називається мішаним числом.
Наприклад.  – мішане число.
– мішане число.
Для того, щоб подати неправильний дріб, більший від одиниці, у вигляді мішаного числа, треба чисельник дробу поділити на знаменник; в частці дістанемо число цілих одиниць, а в остачі — число відповідних часток одиниці.
Наприклад.  – мішане число.
– мішане число.
І навпаки, щоб подати мішане число у вигляді неправильного дробу, треба цілу частину помножити на знаменник дробової частини і додати чисельник, одержаний результат взяти чисельником і підписати знаменник дробової частини.
Наприклад. 
Віднімання невід’ємних раціональних чисел
Як і для натуральних чисел, віднімання невід’ємних раціональних чисел – дія, обернена додаванню.
Означення.Відняти від раціонального числа  число
число 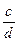 , або знайти різницю
, або знайти різницю 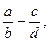 означає знайти таке число
означає знайти таке число 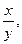 щоб задовольнялась умова
щоб задовольнялась умова 
Множення невід’ємних раціональних чисел
Як відомо, множення цілого невід’ємного числа на натуральне число, більше за 1, зводиться, за означенням, до додавання рівних доданків:

при п = 1 а · 1 = а; при п = 0 а · 0 = 0.
Ці означення поширюють і на випадок множення дробового числа на натуральне число п.
Означення.Добутком дробового числа  на натуральне число п > 1 називається сума п доданків, кожний з яких є
на натуральне число п > 1 називається сума п доданків, кожний з яких є  .
.

Отже, 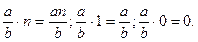
Наприклад. 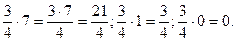
Означення.Добутком невід’ємних раціональних чисел, поданих у вигляді дробів  і
і 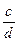 , називається число, зображене дробом, чисельником якого є добуток чисельників даних дробів, а знаменником — добуток знаменників:
, називається число, зображене дробом, чисельником якого є добуток чисельників даних дробів, а знаменником — добуток знаменників:
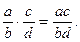
Це означення поширюється і на випадок, коли один чи обидва співмножники є цілі числа, зокрема нуль або 1. Тоді:
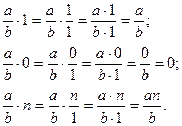
Означення.Два числа, добуток яких дорівнює 1, називаються взаємно оберненими.
Число 1 обернене самому собі, бо 1 · 1 = 1.
Натуральне число п має обернене число 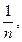 бо
бо 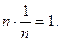 Отже, п і
Отже, п і 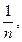 - пара взаємно обернених чисел.
- пара взаємно обернених чисел.
Число  має обернене
має обернене 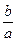 , бо
, бо 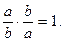 Отже,
Отже,  і
і 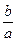 - пара взаємно обернених чисел.
- пара взаємно обернених чисел.
Нуль не має оберненого числа, бо не існує такого числа, яке б при множенні на нуль дало 1.
Читайте також:
- CMM. Визначення моделі зрілості.
- I визначення впливу окремих факторів
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- Ocнoвнi визначення здоров'я
- S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
- А. Визначення розмірів і площі зони хімічного зараження.
- Алгебраїчний спосіб визначення точки беззбитковості
- Алгоритм визначення проекцій точок на поверхнях обертання
- Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
- Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
- Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
| <== попередня сторінка | | | наступна сторінка ==> |
| Дроби та їх властивості | | | Ділення невід’ємного раціонального числа на додатне |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |