• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Несумірні відрізки і ірраціональні числа. Невід’ємні дійсні числа

Нехай маємо деякий відрізок а і певну одиницю виміру е.

Як зазначалося, може бути 2 випадки:

1) одиничний відрізок е вкладається ціле число, наприклад п разів, у відрізку а, і тоді вважають, що довжина відрізка а дорівнює пе: а = пе;

2) одиничний відрізок е не вкладається у відрізку а ціле число разів, тобто після п відкладань залишиться деякий відрізок – остача r < e. Тоді можна записати, що , де r < e.

Природно поставити запитання, яку нову, меншу за е, але пов’язану з е, одиницю виміру слід узяти, щоб вкладалася ціле число разів у відрізку а? Чи завжди має розв’язок ця задача?

Якщо відрізок а сумірний з е, то а виражається через е раціональним числом 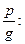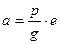, тобто спільною мірою відрізків а і е буде відрізок .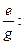

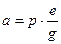Якщо відрізки а і е не матимуть спільної міри, то довжину а не можна виразити через е ніяким раціональним числом. У зв’язку з цим множину раціональних чисел розширено введенням нових чисел, які назвали ірраціональними (не раціональними).

Слово «ratio» латинською мовою означає «відношення», тобто будь-яке раціональне число можна зобразити у вигляді відношення двох цілих чисел: 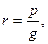де g ≠ 0. Ірраціональне число не можна зобразити у вигляді відношення двох цілих чисел.

Існування несумірних відрізків виявили ще піфагорійці (VI ст. до н.е.), але вони не ввели ірраціональних чисел для їх вимірювання, бо вважали, що довжина – величина неперервна, а число – дискретна (розривна). У відкритті несумірних відрізків вони вбачали «велику таємницю», розголошення якої переслідувалось і «каралося богом».

У «Началах» Евкліда також ірраціональні числа фактично не використовувались. Вперше свідомо почали оперувати ірраціональними числами індійські та китайські математики, переносячи на них усі правила дій над коренями, що являють собою раціональні числа.

Означення. Ірраціональними числами називають числа, які можна зобразити нескінченними десятковими неперіодичними дробами.

Внаслідок розширення множини невід’ємних раціональних чисел введенням ірраціональних (додатних) чисел стала завжди можливою задача вимірювання відрізків: тепер кожній точці числового променя можна поставити у відповідність тільки одне дійсне число (раціональне чи ірраціональне), і навпаки. Саме в цьому і полягає ідея неперервності числового променя і множини невід’ємних дійсних чисел. Між множиною невід’ємних дійсних чисел і множиною точок числового променя існує взаємно однозначна відповідність.

Два ірраціональних числа вважають рівними, якщо вони виражають довжини рівних між собою відрізків.

У множині дійсних невід’ємних чисел зберігаються основні властивості відношень «рівно», «більше», «менше», які було встановлено для невід’ємних раціональних чисел.

Читайте також:

1. II. Множення круглих багатоцифрових чисел на розрядні числа.
2. Абсолютна величина дійсного числа
3. Абсолютна величина числа позначається символом .
4. Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
5. Арифметичні дії над дійсними невід’ємними числами. Їхні властивості
6. Арифметичні операції над цілими числами
7. Визначення арифметичних дій над додатними раціональними числами
8. Визначення добутку двох цілих невід’ємних чисел як числа елементів декартового добутку двох скінченних множин
9. Визначення йодного числа жиру методом Війса.
10. Визначення йодного числа жиру прискореним методом (методом Маргошеса).
11. Визначення йодного числа методом Гюбля.
12. Визначення йодного числа методом Кауфмана

Переглядів: 1437