
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ПЛОСКОГО ПЕРЕРІЗУ
При розрахунках на міцність, жорсткість та стійкість недостатньо знати тільки форму та характерні розміри поперечного перерізу. Потрібні ще й інші геометричні характеристики плоских перерізів, деякі з них ми й розглянемо для перерізу довільної форми, наведеного на рис. 3.1, де через 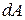 позначено площу виділеного малого елемента.
позначено площу виділеного малого елемента.

Рис. 3.1
І. Площа перерізу:
 ;
;  >0, м2. (3.1)
>0, м2. (3.1)
ІІ. Статичні моменти перерізу (моменти площі) відносно осей 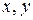 :
:
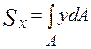 ,
, 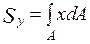 ;
; 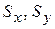 ≥ 0 і
≥ 0 і 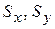 £ 0, м3. (3.2)
£ 0, м3. (3.2)
Осі, що проходять через центр ваги перерізу, називають центральними. Відносно цих осей статичні моменти завжди дорівнюють нулю ( 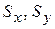 =0). Якщо відомі площа (
=0). Якщо відомі площа (  ) та статичні моменти (
) та статичні моменти ( 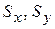 ), то координати центра ваги перерізу (
), то координати центра ваги перерізу ( 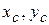 ) в системі координат
) в системі координат  визначаться за наступними формулами:
визначаться за наступними формулами:
 ,
, 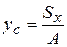 . (3.3)
. (3.3)
ІІІ. Осьові ( 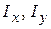 ) та відцентровий (
) та відцентровий (  ) моменти інерції перерізу відносно осей
) моменти інерції перерізу відносно осей 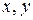 :
:
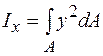 ,
,  ,
, 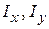 >0, м4; (3.4)
>0, м4; (3.4)
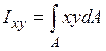 ,
, 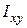 ≥ 0 і
≥ 0 і  £ 0, м4. (3.5)
£ 0, м4. (3.5)
Дві взаємно перпендикулярні осі ( 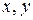 ), відносно яких відцентровий момент інерції дорівнює нулю (
), відносно яких відцентровий момент інерції дорівнює нулю ( 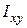 = 0), називають головними.
= 0), називають головними.
Головні осі, які проходять через центр ваги перерізу, називають головними центральними осями інерції (ГЦО). В більшості випадків потрібно знати геометричні характеристики саме відносно ГЦО. Треба пам’ятати, що ось (вісь) симетрії завжди є однією з ГЦО, друга ГЦО пройде через центр ваги перерізу й буде перпендикулярною до осі симетрії.
ІV. Полярний момент інерції перерізу відносно початку координат (точки 0):
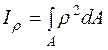 ,
, 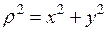 ,
, 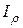 >0, м4. (3.6)
>0, м4. (3.6)
Окрім вищенаведених геометричних характеристик, які називають основними, нам в подальшому знадобляться ще й наступні:
V. Радіуси інерції перерізу відносно осей 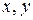 :
:
 ,
,  >0, м. (3.7)
>0, м. (3.7)
VІ. Осьові моменти опору перерізу відносно осей 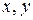 :
:
 ,
, 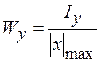 ,
,  ,
,  >0, м3. (3.8)
>0, м3. (3.8)
Тут 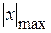 ,
, 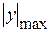 - відстані до точок, найвіддаленіших відповідно від осей
- відстані до точок, найвіддаленіших відповідно від осей 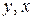 .
.
VІІ. Полярний момент опору перерізу:
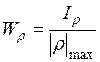 ,
, 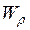 >0, м3. (3.9)
>0, м3. (3.9)
де  - відстань від центра ваги або початку координат до найвіддаленішої точки перерізу.
- відстань від центра ваги або початку координат до найвіддаленішої точки перерізу.
Формули для визначення геометричних характеристик деяких нестандартних перерізів наведені нижче:
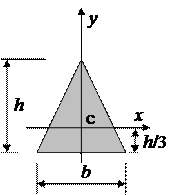 1. Рівнобедрений трикутник 1. Рівнобедрений трикутник
| Площа:  .
Осьові моменти інерції: .
Осьові моменти інерції:
 ; ; 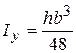 .
Радіуси інерції: .
Радіуси інерції: 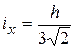 ; ; 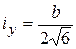 .
Ось .
Ось 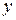 - це вісь симетрії, тому осі - це вісь симетрії, тому осі 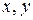 є головними центральними осями і відцентровий момент інерції є головними центральними осями і відцентровий момент інерції  . .
|
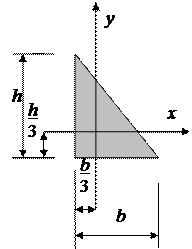 2. Прямокутний трикутник
с 2. Прямокутний трикутник
с
| Площа  .
Осьові моменти інерції .
Осьові моменти інерції  ; ; 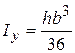 .
Осі .
Осі  - це центральні, але неголовні осі інерції, тому відносно їх відцентровий момент інерції не дорівнює нулю: - це центральні, але неголовні осі інерції, тому відносно їх відцентровий момент інерції не дорівнює нулю:
 .
Якщо додатні напрями осей .
Якщо додатні напрями осей 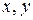 одночасно перетинають гіпотенузу або обидва катети, то у виразі для визначення одночасно перетинають гіпотенузу або обидва катети, то у виразі для визначення 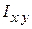 треба утримати знак «-». треба утримати знак «-».
|
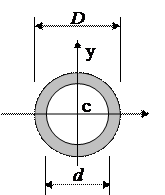 3. Кільце та круг
x 3. Кільце та круг
x
| Осі 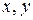 - це головні центральні осі, тому що вони являються осями симетрії.
Площа: - це головні центральні осі, тому що вони являються осями симетрії.
Площа: 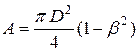 .
Тут і далі .
Тут і далі 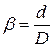 ; для круга ; для круга 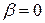 .
Осьовий момент інерції: .
Осьовий момент інерції:
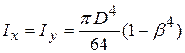 .
Полярний момент інерції .
Полярний момент інерції  .
Осьовий момент опору: .
Осьовий момент опору:
 .
Полярний момент опору: .
Полярний момент опору:  .
Радіус інерції: .
Радіус інерції: 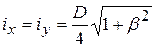 .
Відцентровий момент інерції .
Відцентровий момент інерції  . .
|
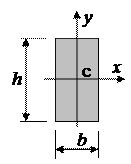 4. Прямокутник 4. Прямокутник
| Площа 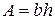 .
Осьові моменти інерції: .
Осьові моменти інерції:
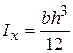 ; ; 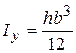 .
Осьові моменти опору: .
Осьові моменти опору:
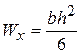 ; ; 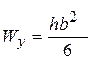 .
Радіуси інерції: .
Радіуси інерції: 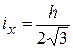 ; ;  .
Осі .
Осі 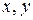 - це головні центральні осі (вони являються осями симетрії), тому відцентровий момент інерції - це головні центральні осі (вони являються осями симетрії), тому відцентровий момент інерції  . .
|
Для геометричних характеристик використовуються такі теореми, властивості та формули:
1. Теорема про геометричні характеристики складного перерізу.
Геометрична характеристика складного перерізу дорівнює алгебраїчній сумі відповідних геометричних характеристик простих фігур, з яких складається складний переріз.
2. Теорема про постійність суми осьових моментів інерції відносно будь-яких взаємно перпендикулярних осей, що проходять через задану точку (властивість інваріантності).
Сума осьових моментів інерції відносно будь-яких взаємно перпендикулярних осей (рис. 3.2), що проходять через задану точку (початок координат), – величина стала і дорівнює полярному моменту інерції відносно початку координат:
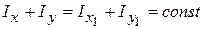 . (3.10)
. (3.10)
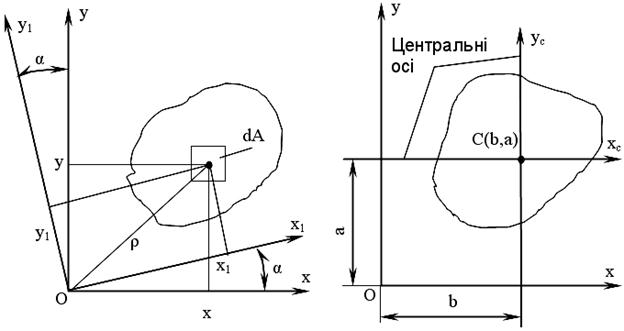
Рис.3.2 Рис.3.3
3. Теорема про осьові та відцентровий моменти інерції відносно нецентральних осей, які паралельні центральним осям перерізу (рис. 3.3).
Осьовий момент інерції відносно будь-якої нецентральної осі, яка паралельна центральній, дорівнює осьовому моменту інерції відносно центральної осі плюс добуток квадрату найменшої відстані між вказаними осями ( 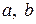 ) на площу перерізу:
) на площу перерізу:
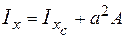 ,
, 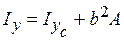 . (3.11)
. (3.11)
Відцентровий момент інерції відносно взаємно перпендикулярних нецентральних осей, що паралельні центральним, дорівнює відцентровому моменту інерції відносно центральних осей плюс добуток координат центра ваги перерізу в нецентральних осях (згадані найменші відстані між паралельними осями - 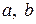 ) на площу перерізу:
) на площу перерізу:
 . (3.12)
. (3.12)
4. Теорема про властивість відцентрового моменту інерції при заміні напряму однієї з осей на протилежний.
При заміні напряму однієї з осей (  ) на протилежний (
) на протилежний ( 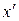 ) відцентровий момент інерції змінює знак на протилежний:
) відцентровий момент інерції змінює знак на протилежний:
 . (3.13)
. (3.13)
5. Залежності між моментами інерції при повороті осей навколо початку координат (0) на кут 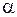 (рис.3.2):
(рис.3.2):
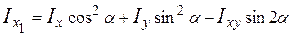 ,
,
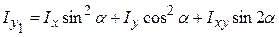 , (3.14)
, (3.14)
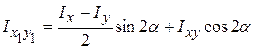 .
.
При дослідженні геометричних характеристик плоского перерізу однією з основних задач є визначення положення головних центральних осей інерції перерізу та деяких геометричних характеристик, що зв’язані з цими осями.
Як вже відмічалося раніше, головними центральними осями (ГЦО) інерції перерізу називаються такі дві взаємно перпендикулярні центральні осі, відносно яких відцентровий момент інерції дорівнює нулю, а осьові моменти інерції (які називаються головними центральними моментами інерції) мають екстремальні значення  . Положення головних центральних осей (
. Положення головних центральних осей ( 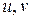 ) відносно будь-яких центральних осей
) відносно будь-яких центральних осей 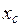 ,
,  визначаються кутами
визначаються кутами  та
та  , що знаходяться за формулою
, що знаходяться за формулою
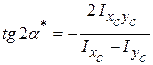 (3.15)
(3.15)
(додатний кут  відкладається від осі
відкладається від осі 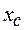 проти ходу годинникової стрілки, а від’ємний – за ходом вказаної стрілки).
проти ходу годинникової стрілки, а від’ємний – за ходом вказаної стрілки).
Головні центральні осьові моменти інерції перерізу  (осьові моменти інерції відносно головних центральних осей) визначаються за формулою
(осьові моменти інерції відносно головних центральних осей) визначаються за формулою
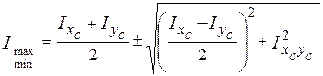 , (3.16)
, (3.16)
де знак “+” відповідає 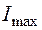 , а знак “–“ відповідає
, а знак “–“ відповідає 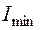 .
.
Приклад розв’язання задачі № 4. На рис. 3.4 зображено поперечний переріз елемента конструкції, який складається з таких прокатних профілів: (швелера) [№24 за ГОСТ 8240-89, (нерівнобокого (нерівнополочного) кутника) L125х80х8 за ГОСТ 8510-86 і (листа (штаби)) ––200х20. Для вказаного перерізу потрібно визначити наступне: а) положення центра ваги (  ); б) моменти інерції перерізу відносно допоміжних центральних осей (
); б) моменти інерції перерізу відносно допоміжних центральних осей ( 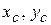 ); в) положення головних центральних осей (
); в) положення головних центральних осей ( 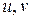 ) відносно допоміжних центральних осей (
) відносно допоміжних центральних осей ( 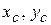 ); г) головні центральні осьові моменти інерції (
); г) головні центральні осьові моменти інерції (  ), осьові моменти опору (
), осьові моменти опору (  ,
,  ) та радіуси інерції перерізу (
) та радіуси інерції перерізу (  ).
).
Зауваження. Номер швелера та двотавра – це їх висота (  ) в см; у кутника два перших розміри – це дві ширини полиць, а третій розмір – це товщини полиць, розміри наводяться в мм; поперечні перерізи листа або штаби являють собою прямокутник, для якого наводяться його ширина та висота (товщина) в мм.
) в см; у кутника два перших розміри – це дві ширини полиць, а третій розмір – це товщини полиць, розміри наводяться в мм; поперечні перерізи листа або штаби являють собою прямокутник, для якого наводяться його ширина та висота (товщина) в мм.
Через центри ваги елементів складного перерізу (  ) проводимо власні центральні осі так, щоб осі абсцис і ординат були відповідно паралельними. Відносно вказаних осей моменти інерції кожного з елементів повинні бути відомими з таблиць сортаменту або відомі формули для їх визначення.
) проводимо власні центральні осі так, щоб осі абсцис і ординат були відповідно паралельними. Відносно вказаних осей моменти інерції кожного з елементів повинні бути відомими з таблиць сортаменту або відомі формули для їх визначення.
Так, для [ №24 з таблиці сортаменту маємо  =30,6 см2,
=30,6 см2,  =2900 см4,
=2900 см4,  =208 см4,
=208 см4, 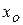 =2,42 см. Відцентровий момент інерції дорівнює нулю (
=2,42 см. Відцентровий момент інерції дорівнює нулю ( 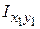 =0), тому що одна з двох центральних взаємно перпендикулярних осей є вісь симетрії (
=0), тому що одна з двох центральних взаємно перпендикулярних осей є вісь симетрії ( 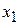 ).
).
Для L 125х80х8 з таблиці сортаменту маємо 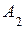 =16 см2,
=16 см2, 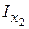 =256 см4,
=256 см4,  =83 см4,
=83 см4, 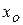 =1,84 см,
=1,84 см,  =4,05 см і
=4,05 см і 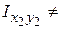 0.
0.
В деяких таблицях сортаменту наведено тільки значення  , де
, де 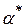 - кут, який визначає положення головних центральних осей кутника відносно заданих неголовних центральних осей
- кут, який визначає положення головних центральних осей кутника відносно заданих неголовних центральних осей 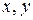 . Скориставшись відомою формулою
. Скориставшись відомою формулою 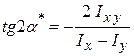 , для загального випадку орієнтації нерівнобокого кутника отримаємо таку формулу:
, для загального випадку орієнтації нерівнобокого кутника отримаємо таку формулу:
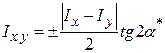 .
.
Знак вибирається за наступним правилом:

Для розглядуваного кутника  ,
, 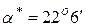 ,
, 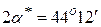 ,
, 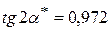 і відцентровий момент інерції буде від’ємним:
і відцентровий момент інерції буде від’ємним:
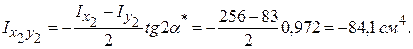
В деяких же таблицях сортаменту наведено абсолютне значення відцентрового моменту і треба тільки встановити його знак, згідно з вищенаведеним правилом для кутників.
Зауваження. Якщо кутник рівнобокий, то
 .
.
Значення  наводяться в таблицях сортаменту, а знак вибирається згідно з вищенаведеним правилом.
наводяться в таблицях сортаменту, а знак вибирається згідно з вищенаведеним правилом.
Для –– 200х20 приймаємо 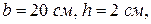 тоді, згідно з формулами для визначення геометричних характеристик прямокутника, маємо наступне:
тоді, згідно з формулами для визначення геометричних характеристик прямокутника, маємо наступне:

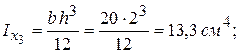

Координати центра ваги (точки С) складного перерізу відносно якихось вихідних осей 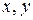 у визначаються за наступними формулами:
у визначаються за наступними формулами:
 ,
, 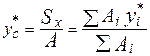 ;
;
де 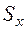 ,
, 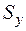 – статичні моменти (моменти площі) перерізу відносно вихідних осей
– статичні моменти (моменти площі) перерізу відносно вихідних осей 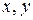 ;
; 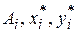 – площа та координати центра ваги i-го елемента відносно осей
– площа та координати центра ваги i-го елемента відносно осей 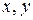 . За початкові осі доцільно обирати власні центральні осі одного з елементів складного перерізу.
. За початкові осі доцільно обирати власні центральні осі одного з елементів складного перерізу.
При розв’язанні цієї задачі за початкові осі приймаємо центральні осі швелера  . Визначимо координати центрів ваги елементів складного перерізу (
. Визначимо координати центрів ваги елементів складного перерізу (  ) в системі координат
) в системі координат  :
:
для швелера 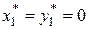 ;
;
для кутника 
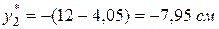 ;
;
для прямокутника (листа, штаби) 
 .
.
Загальна площа складного перерізу
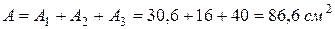 .
.
Далі визначимо координати центра ваги (С) складного перерізу в системі координат  :
:
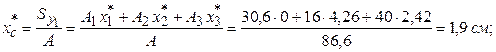

В системі координат  відкладаємо знайдені координати
відкладаємо знайдені координати  , з урахуванням масштабу та знаків, і будуємо центр ваги складного перерізу С, а потім через нього проводимо центральні осі
, з урахуванням масштабу та знаків, і будуємо центр ваги складного перерізу С, а потім через нього проводимо центральні осі 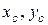 (рис. 3.4).
(рис. 3.4).
Осьові та відцентровий моменти інерції перерізу відносно центральних осей хс, ус визначаються за наступними формулами:
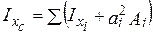 ,
,  ,
, 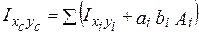 ;
;
де  - осьові та відцентровий моменти інерції i-го елемента перерізу відносно власних центральних осей хі та уі , паралельних центральним осям складного перерізу
- осьові та відцентровий моменти інерції i-го елемента перерізу відносно власних центральних осей хі та уі , паралельних центральним осям складного перерізу  ;
; 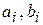 – координати центра ваги і–го елемента в системі координат хсСус.
– координати центра ваги і–го елемента в системі координат хсСус.
За допомогою рис. 3.4 і даних про положення центрів ваги кожного з елементів, наведених вище, визначимо координати 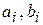 :
: 

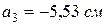 і
і 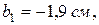


Далі визначимо осьові та відцентровий моменти інерції перерізу відносно центральних осей 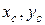 :
:

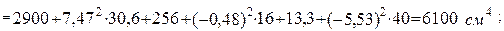

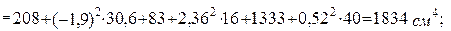
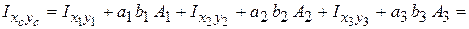

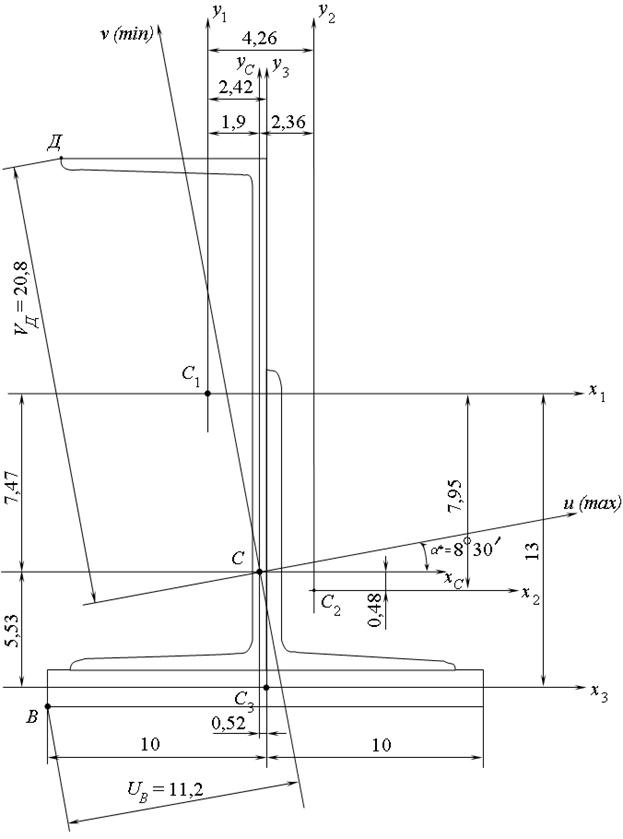
М 1: 2 ((указати обраний Вами масштаб)
Розміри в см
Рис. 3.4
Положення однієї з головних центральних осей відносно горизонтальної центральної осі 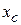 визначається кутом
визначається кутом 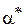 . Визначимо цей кут для нашого складного перерізу
. Визначимо цей кут для нашого складного перерізу

 і
і  .
.
Перевіримо правильність визначення кута 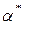 . Скористаємось умовою, що відносно любих головних осей відцентровий момент інерції повинен дорівнювати нулю, тобто
. Скористаємось умовою, що відносно любих головних осей відцентровий момент інерції повинен дорівнювати нулю, тобто
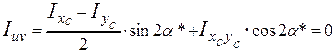 ,
,
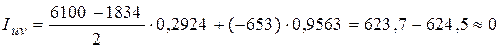 .
.
Під кутами  і
і  до осі
до осі 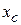 проводимо головні центральні осі
проводимо головні центральні осі  та
та  (див. рис. 3.4). Кут
(див. рис. 3.4). Кут 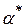 додатний, тому його відкладено від осі
додатний, тому його відкладено від осі 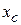 проти ходу годинникової стрілки. Щоб встановити, яка з них відповідає осі
проти ходу годинникової стрілки. Щоб встановити, яка з них відповідає осі 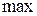 (з
(з 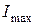 ), а яка – осі
), а яка – осі  (з
(з  ), скористаємося таким правилом: якщо
), скористаємося таким правилом: якщо  < 0, то ось
< 0, то ось 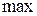 пройде через перший та третій квадранти, а ось
пройде через перший та третій квадранти, а ось  – через другий та четвертий квадранти (наш випадок); якщо
– через другий та четвертий квадранти (наш випадок); якщо  > 0, то ось
> 0, то ось 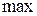 пройде через другий та четвертий квадранти, а ось
пройде через другий та четвертий квадранти, а ось  – через перший та третій.
– через перший та третій.
Головна центральна ось, відносно якої осьовий момент інерції набуває значення  , спрямована в бік витягнутості перерізу, а головна центральна ось, відносно якої осьовий момент інерції набуває значення
, спрямована в бік витягнутості перерізу, а головна центральна ось, відносно якої осьовий момент інерції набуває значення 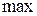 – в бік стиснутості перерізу.
– в бік стиснутості перерізу.
Згідно з викладеним правилом встановлюємо, що ось  відповідає осі
відповідає осі 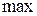 , а ось
, а ось  – осі
– осі  .
.
Потім визначаємо головні центральні осьові моменти інерції:
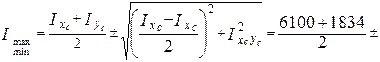

і 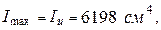
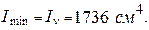
Бачимо, що екстремальність головних центральних моментів інерції 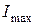 ,
,  відносно
відносно 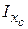 ,
,  виконується. Далі перевіримо виконання теореми про постійність суми осьових моментів інерції відносно будь-яких взаємно перпендикулярних осей, що проходять через задану точку (властивість інваріантності):
виконується. Далі перевіримо виконання теореми про постійність суми осьових моментів інерції відносно будь-яких взаємно перпендикулярних осей, що проходять через задану точку (властивість інваріантності):
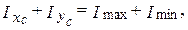
 , 7934≡7934.
, 7934≡7934.
Теорема виконується.
По рис. 3.4 встановлюємо, що від осі  найвіддалена точка Д з координатою
найвіддалена точка Д з координатою 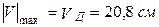 , а від осі
, а від осі  найвіддалена точка В з координатою
найвіддалена точка В з координатою 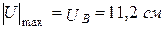 . Тоді осьові моменти опору перерізу відносно головних центральних осей
. Тоді осьові моменти опору перерізу відносно головних центральних осей  та
та  визначаться за формулами
визначаться за формулами
 і
і 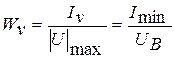 .
.
Отже

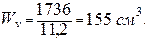
Головні центральні радіуси інерції перерізу такі
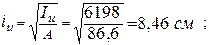

Контрольні запитання
1. Що відноситься до геометричних характеристик плоского перерізу?
2. Як у загальному випадку записуються вирази для визначення основних геометричних характеристик довільного перерізу?
3. Як записуються вирази для визначення моментів опору та радіусів інерції перерізу?
4. Як формулюються основні теореми про геометричні характеристики?
5. Які існують залежності між моментами інерції при повороті осей координат?
6. Як знайти положення центра ваги перерізу відносно відомих осей координат?
7. Які осі називають головними та головними центральними?
8. Як знайти положення головних центральних осей відносно відомих неголовних центральних осей координат?
9. Як визначаються головні осьові моменти інерції?
10. У якій послідовності визначаються геометричні характеристики складних перерізів?
11. Як спрощується визначення положення головних центральних осей, якщо переріз має одну чи декілька осей симетрії?
12. За якими формулами визначаються основні геометричні характеристики для кругового, кільцевого, прямокутного та трикутних перерізів?
13. Які геометричні характеристики для стандартних прокатних профілів наведено у відповідних таблицях сортаменту?
ЗАДАЧІ № 5а та № 5б
Читайте також:
- Вибір перерізу повітряних ліній
- Вибір перерізу провідників у мережах напругою до 1000 В з урахуванням плавких запобіжників
- Вибір перерізу провідників у мережах напругою до 1000В з урахуванням автоматичних вимикачів і теплових реле
- Визначення площі перерізу арматури
- Визначення потрібної площі перерізу стояка.
- Визначення розмірів поперечного перерізу колони
- Втискування плоского циліндричного індентора
- Геометричні характеристики поперечного перерізу
- Головні осі інерції та головні моменти інерції перерізу
- Головні осі інерції та головні моменти інерції перерізу
- Ємність плоского конденсатора.
- Загальні випадки перерізу
| <== попередня сторінка | | | наступна сторінка ==> |
| ЗАДАЧА № 4 | | | РОЗРАХУНОК СТАТИЧНО ВИЗНАЧЕНИХ БАЛОК НА МІЦНІСТЬ ПРИ ПЛОСКОМУ ЗГИНІ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |