• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Напруження при плоскому поперечному згині

Нормальні напруження ( 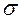) в будь-якій точці довільного поперечного перерізу балки визначають за формулою, отриманою Нав’є:

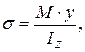(4.2)

де М – згинаючий момент в розглядуваному перерізі балки; 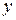– ордината розглядуваної точки (відстань від нейтральної лінії (осі 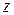) до точки, яка відкладається з урахуванням знаку); 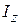– осьовий момент інерції поперечного перерізу відносно головної центральної осі .

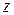Ця формула отримана для випадку чистого плоского згину, але в багатьох випадках придатна й для плоского поперечного згину (коли впливом поперечних сил на згинаючі моменти та деформації балки можна знехтувати).

З виразу (4.2) видно, що знак 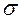визначається знаками М та 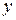, що нормальні напруження по ширині поперечного перерізу розподілені рівномірно ( 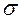не залежить від 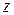), а по висоті нормальні напруження змінюються за лінійним законом (законом прямої лінії), зокрема, при y=0 вони відсутні (звідси й назви – нейтральна лінія в поперечному перерізі, нейтральний шар балки). Найбільші нормальні напруження виникають в крайніх точках перерізу, найвіддаленіших від нейтральної лінії (в небезпечних точках при ):

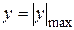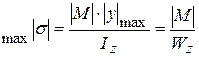. (4.3)

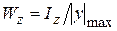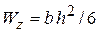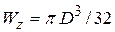Тут – осьовий момент опору поперечного перерізу балки (для прямокутного перерізу , де - ширина, а - висота прямокутника; для кругового перерізу , де 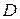- діаметр перерізу; для прокатних двотаврів і швелерів осьові моменти опору наведені у відповідних таблицях сортаменту й при раціональній орієнтації перерізу балки ).

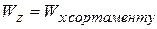Для визначення дотичних напружень в будь-якій точці довільного поперечного перерізу балки застосовується формула Д.І. Журавського:

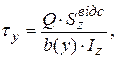(4.4)

де 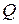– поперечна сила в перерізі; 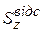– статичний момент відсіченої частини поперечного перерізу балки відносно осі 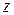, тобто частини, що розташована по один бік від точки, для якої визначається дотичне напруження (береться абсолютне значення статичного моменту; частина перерізу відсікається лінією, паралельною осі 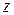); 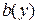– ширина перерізу в місці розташування точки, в якій визначається дотичне напруження; 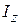– осьовий момент інерції поперечного перерізу відносно головної центральної осі інерції .

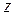З виразу (4.4) видно, що знак 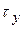визначається знаком 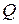, що дотичні напруження по ширині поперечного перерізу розподілені рівномірно ( 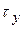не залежать від ).

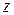Дотичні напруження по висоті перерізу змінюються за параболічним законом й для більшості видів перерізів досягають максимальних за абсолютним значенням величин на нейтральній лінії (в небезпечних точках при y=0):

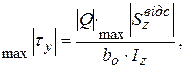(4.5)

де 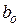– ширина перерізу при 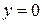; 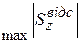– статичний момент однієї з частин площі поперечного перерізу, яка відсікається віссю 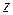, відносно цієї ж осі; у випадку бісиметричного перерізу (двотавровий, прямокутний) 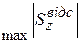– це статичний момент половини площі перерізу відносно осі 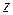. Для прокатних двотаврів і швелерів .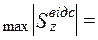

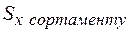Читайте також:

1. Бруса малої кривини при згині
2. Визначення втрат попереднього напруження
3. Визначення зусилля попереднього обтиску і величини попереднього напруження
4. Внутрішні сили при плоскому згині.
5. Вправи для зняття м'язового напруження
6. Головні напруження та головні площадки.
7. Головні площадки і головні напруження
8. Допустиме напруження
9. Методика розрахунку по граничному стану, та за граничними напруженнями.
10. М’язове перенапруження.
11. Наповнення і напруження
12. Напруження в перерізі

Переглядів: 2536