• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Загальна постановки задачі

Мається деякий склад для збереження 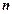найменувань товарів. Відомий щоденний попит на кожен вид товарів Відома загальна ємність (місткість) складу 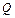. Потрібно визначити процедуру завезення товарів на склад, при якій попит задовольняється і витрати мінімальні. Нехай – обсяги партій відповідних товарів. Їхню суму позначимо через ,

У моделі без дефіциту витрати двох видів:

1. витрати за замовленням і доставкою товарів;

2. витрати збереження;

Задача має тривіальне рішення.

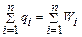
Недоліки цього рішення:

1. склад працює як перевалочна база;

2. неможливість реалізації рішення на практиці:

а) для багатьох видів товарів існують мінімальні обсяги партій;

б) загальний обсяг може бути занадто великий для одночасної доставки (транспортне обмеження).

Висновок: для реального працюючого складу (оптової бази) практично неможливе одноразове завезення за всією номенклатурою товарів.

Формулювання однієї з конкретних задач – визначити графік доставки товарів у такій черговості й у такій кількості, щоб при безумовному задоволенні попиту середньої обсяг (рівень) запасів був мінімальним.

Математичні методи розв’язання подібних задач створюють теорію управління запасами.

Однопродуктова модель Уїлсона:

1. на складі зберігається один товар (продукт);

2. попит на товар є постійним (рівень запасу товару зменшується з постійною швидкістю) ;

3. у той момент, коли запас вичерпаний, подається заявка на доставку нової партії товарів;

4. виконання заявки (замовлення) здійснюється миттєво;

5. накладні витрати, пов'язані з замовленням і доставкою товару постійні і не залежать від кількості товарів (обсягу партій) ;

6. щоденна вартість збереження одиниці товару
постійна С₁.

Схема роботи складу

– максимальна кількість товару на складі; – час; – інтервал часу між точками замовлення.

;

3.Плануємо роботу складу на деякий період Т

Розраховуємо кількість замовлень: .

Загальні витрати за замовленням і доставкою:

Середній рівень запасу:

Витрати на збереження в одному періоді: .

Загальні витрати на збереження:

Загальні витрати в плановому періоді S:

,

(8.1)

Знайдемо мінімум складеної функції витрат.

; ; .

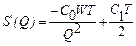Формула Уїлсона: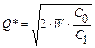

(8.2)

Можна перевірити, що Q* - це точка мінімуму:

(8.3)

(8.4)

Висновок: у точці мінімуму витрати збереження дорівнюють витратам на замовлення і доставку.

(8.5)

Знайдемо інтервал між замовленнями.

(8.6)

Практичні труднощі при використанні моделі Уїлсона:

1. теоретична оптимальна величина не завжди може бути реалізована на практиці. Округлення в будь-яку сторону приводить до збільшення витрат порівняно з мінімально теоретично можливими.

2. оптимальне також може бути практично не реалізованим.

Напрямки ускладнення моделі Уїлсона:

1. Модель з дефіцитом.

2. – змінний детермінований попит.

3. Моделі з випадковим попитом

4. Багатопродуктові моделі.

Читайте також:

1. I. Загальна характеристика політичної та правової думки античної Греції.
2. IV. Загальна оцінка діяльності вчителя
3. IV. Загальна схема поточного і підсумкового контролю та оцінювання знань студентів
4. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
5. А) Задачі, що розкривають зміст дій
6. Алгоритм розв’язання задачі
7. Алгоритм розв’язання задачі
8. Алгоритм розв’язання розподільної задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі
12. Алгоритм розв’язування задачі

Переглядів: 369