• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Однопродуктова модель з дефіцитом

– постійний попит, і – ті ж константи моделі,
– період планування. Підлягає визначенню: 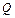– оптимальний розмір партій товарів, 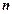–кількість замовлень, – інтервал між замовленнями.

Дозволяємо дефіцит товару, тобто вважається припустимим, що якийсь час товар на складі відсутній. Уводимо величину
– максимальний рівень запасу на складі, тоді максимально припустимий дефіцит.

(8.7)

– склад працює; – товару немає, склад не працює.

(8.8)

(8.9)

Схема роботи складу

Уведемо константу - штраф за непостачання одиниці товару за одиницю часу. Загальні витрати: ,

де – загальні витрати на замовлення і доставку;

– загальні витрати на збереження; – загальна сума штрафів;

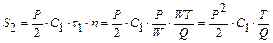
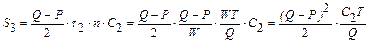
(8.10)

Знайдемо мінімум функції витрат :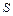

Координати критичної точки:

оптимальний розмір партії

(8.11)

оптимальний максимальний запас

(8.12)

Уведемо спеціальне позначення: – щільність збитків через незадоволений попит.

(8.13)

(8.14)

Це частка часу, коли на складі є товар.

Якщо , то модель бездефіцитна.

	(8.15)
	(8.16)

Якщо , то

При досить великих штрафах дефіцит практично неможливий. Бездефіцитна модель є граничним випадком моделі з дефіцитом.

Контрольні питання

1. Яка загальна постановка задачі управління запасами?

2. Які умови моделі Уїлсона?

3. З чого складаються загальні витрати в цій моделі?

4. Які є недоліки в оптимальному розв’язку задачі?

5. Яким є постановка задачи з дефіцитом?

6. Яким є формули Уїлсона для моделі з дефіцитом?

Лекція 9
Богатопродуктові моделі управління запасами

1. Загальна постановка задачі управління запасами длябагатопродуктового складу

2. Формула Уїлсона для багатопродуктової моделі

3. Загальна задача з обмеженнями: метод множників Лагранжа

4. Задача з обмеженням за середнім рівнем запасу

5. Задача з обмеженням за вартістю запасу

6. Задача з обмеженням витрат на замовлення

7. Модель зі спільними замовленнями

1.Постановка задачі.

Мається склад для збереження продуктів і виконані всі інші умови моделі Уїлсона. Маємо вектор, що задає щоденний попит по всіх видах продуктів , . Задано вектор констант вартості замовлень і доставки товарів 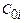; Вектор констант - питомі витрати на збереження. Потрібно розрахувати розміри оптимальних партій по всіх видах товарів.

2.Складається набір функцій витрат Вони мають однотипний вигляд.

,

(9.1)

де – шукана величина – обсяги партій відповідного продукту;

– тривалість періоду планування;

Складається загальна функція витрат (функція 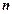змінних):

(9.2)

Розв’язується задача знаходження мінімуму цієї функції.

Для зручності, пропонується ввести нові позначення.

Після введення таких позначень функцію витрат можна записати в наступному вигляді:

(9.3)

Координати критичної точки можна знайти з умов.

(9.4)

Одержимо наступні формули моделі Уїлсона.

(9.5)

Мінімальні витрати:

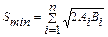
(9.6)

Ці формули придатні для досить великих складів і не містять ніяких обмежень на роботу складу. Реальні багатопродуктові склади мають різні обмеження.

Нехай вектор усіх товарів. Будемо вважати, що в нас є деяка кількість обмежень.

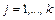
(9.7)

Потрібно знайти мінімум функції (3) за додаткової умови (7). Такі задачі розв’язуються методом множників Лагранжа.

(9.8)

Необхідною умовою мінімуму є система рівнянь, де крім частинних похідних по одній групі змінних містяться похідні по другій групі.

Розглянемо варіанти задач з конкретними видами обмежень:

Читайте також:

1. CMM. Модель технологічної зрілості. Зрілі і незрілі організації.
2. Demo 7: Модель OSI (модель взаімодії відкритих систем)
3. G2G-модель електронного уряду
4. OSI - Базова Еталонна модель взаємодії відкритих систем
5. V – модель
6. Абстрактна модель
7. Абстрактна модель
8. Абстрактна модель оптимального планування виробництва
9. Американська модель соціальної відповідальності
10. Аналіз динаміки ринку, модель життєвого циклу
11. Англійський економіст У. Бріджез пропонує модель організаційних змін за такими напрямками.
12. Англо-американська модель

Переглядів: 423