• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рішення.

Значення швидкості тіла: ,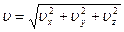

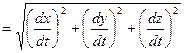Прискорення: ,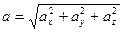

.

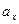
Сила, що діє на тіло: , .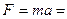

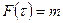
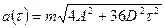Кінетична енергія тіла: ,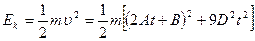

.

Задача 2.Обруч (куля, циліндр), що має масу m і радіус R котиться без прослизання зі швидкість υ. Визначити його кінетичну енергію. Тертям катання зневажити.

Рішення.Кінетична енергія тіла в даному випадку визначається по теоремі Кьоніга:

,

де - момент інерції тіла щодо осі, що проходить через центр інерції, коефіцієнт k залежить від форми тіла. У даному випадку: k =1 – для обруча, k = 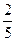- для кулі, k = 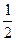– для циліндра.

.

Кутова і лінійна швидкості зв'язані співвідношенням: , отже: для обруча

, для кулі , для циліндра .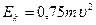

Задача 3.У судині обсягом V знаходиться суміш m₁ газу з молярною масою M ₁ і m₂гази з молярною масою M₂ при температурі T . Визначити тиск p і молярну масу суміші газів M . Універсальна газова постійна R = 8,31 Дж/(моль·К).

Рішення.Запишемо рівняння Менделєєва – Клапейрона для кожного з газів:

, ,

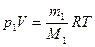де 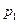- парціальний тиск першого газу, - другого. За законом Дальтона тиск суміші дорівнює сумі парціальних тисків складову суміш газів: ,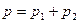

;

.

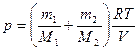Молярна маса суміші: 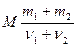, де 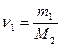- число молів першого газу, 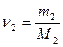- другого. Молярна маса суміші:

.

Задача 4.Обсяг газу, що знаходиться при тиску p₁, збільшився від значення V₁ до значення V₂. Знайти зміна внутрішньої енергії газу, якщо розширення відбулося:

1) изобарически; 2) адиабатически.

Рішення.По першому початку термодинаміки кількість теплоти Q , передане системі, витрачається на збільшення її внутрішньої енергії ΔU і роботу A, чинену газом проти зовнішніх тіл:

,

,

.

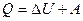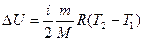Число ступенів волі молекули i дорівнює i =3 для одноатомних молекул, i=5 для двохатомних молекул, i=6 для більш складних молекул.

1) Ізобаричний процес.У цьому випадку тиск постійний 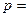const = 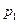. Запишемо рівняння Менделєєва – Клапейрона для початкового і кінцевого стану:

, .

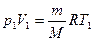Звідси випливає: ,

.

2) Адіабатичний процес.У цьому випадку теплообмін з навколишнім середовищем відсутня 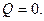Робота відбувається газом за рахунок убули ег внутрішньої енергії

Робота в адіабатичному процесі:

де - показник адіабати, дорівнює відношенню молярних (або питомих) теплоємкостей газу при постійному тиску 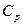і постійному обсязі .

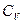Оскільки , та зміна внутрішньої енергії:

.

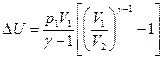Читайте також:

1. Багатокритерійні завдання і можливі шляхи їхнього рішення.
2. Виконання рішення.
3. Відкладення, відстрочка або розстрочка виконання, зміна способу і порядку виконання рішення.
4. Домогосподарства як суб’єкт економічної теорії: проблеми та способи їх вирішення.
5. Завдання вибору критеріїв обґрунтування рішення.
6. Збори як форма прийняття колективного рішення. Нарада. Дискусія
7. Й крок. Оцінити успішність рішення.
8. Класифікація глобальних проблем та проблема їх вирішення.
9. Контроль еиконання управлінського рішення.
10. Крок . Прийняти рішення.
11. Міжнародні економічні аспекти вирішення економічних, продовольчих і ресурсоенергетичних проблем. Шляхи їх вирішення.
12. Місце виконання рішення.

Переглядів: 577