
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Аналіз статистичних залежностей періодичних відліків часу ПФС від температури
3.1. Температурна стійкість інтервалів часу при нелінійних температурних характеристиках ПФС. Розглянемо спосіб розрахунку температурної стійкості часових інтервалів для випадку нелінійної залежності зміни часових інтервалів від температури. Для цього візьмемо вибіркову партію однотипних ПФС і визначимо для кожного ПФС (29 екземплярів) залежність відносного відхилення часових інтервалів  від температури (номінальний інтервал часу між періодичними відліками часу ВПС дорівнює
від температури (номінальний інтервал часу між періодичними відліками часу ВПС дорівнює 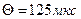 ). На підставі отриманих даних побудуємо сімейство кривих, які перетинаються в точці температури де здійснювалося їхнє настроювання (+20оС) й розбіжних від цієї точки в обидва боки пучків (див. рис.1, де наведено дані для 1-го, 5-го, 7-го, 15-го, 17-го, 22-го та 29-го ПФС).
). На підставі отриманих даних побудуємо сімейство кривих, які перетинаються в точці температури де здійснювалося їхнє настроювання (+20оС) й розбіжних від цієї точки в обидва боки пучків (див. рис.1, де наведено дані для 1-го, 5-го, 7-го, 15-го, 17-го, 22-го та 29-го ПФС).

Рисунок 1 - Залежність відносного відхилення часових інтервалів вибіркової партії однотипних ПФС від температури
Якщо узагальнити результати досліджень усіх ПФС, то можна отримати границі такого пучка. Вказані границі зображені на рис.2 суцільною лінією, а їхнє середнє значення - штрих-пунктиром.
Позначимо аналітичну залежність (рис.2), зображену штрих-пунктиром, деякою функцією m(tо) - середнє значення, а як характеристика ширини пучка для кожного значення tо виберемо середньоквадратичне відхилення, що, очевидно, залежить від температури й може бути у зв'язку із цим виражено деякою функцією d(tо).
Тепер розглянемо розподіл ймовірностей відхилень часових інтервалів під впливом температури для всієї множини ПФС досліджуваної партії за термін їхньої експлуатації в реальних умовах. При цьому будемо вважати розподіл робочої температури рівновірогідним у межах інтервалу  . Відповідно даному розподілу щільність ймовірностей окремих значень температурної стійкості часових інтервалів ПФС для всієї партії позначимо функцією
. Відповідно даному розподілу щільність ймовірностей окремих значень температурної стійкості часових інтервалів ПФС для всієї партії позначимо функцією 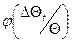 . Загалом, функцію
. Загалом, функцію 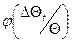 можна розглядати як розподіл об’єднаних багатьох складових частин, що мають однаковий об’єм і досить вузькі інтервали робочої температури, у межі на ділянці dtо.
можна розглядати як розподіл об’єднаних багатьох складових частин, що мають однаковий об’єм і досить вузькі інтервали робочої температури, у межі на ділянці dtо.

Щільності ймовірностей для кожної з таких частин будуть різними, тому що ділянки dtо розташовані в різних місцях осі tо. Однак всі вони можуть бути виражені деяким функціоналом з середнім значенням - m(tо) та функцією - d(tо) як параметри, що позначимо  . Цей функціонал на кожному інтервалі температури tо здобуває форму [1]:
. Цей функціонал на кожному інтервалі температури tо здобуває форму [1]:
 (2)
(2)
Оскільки середнє значення 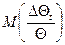 й дисперсія
й дисперсія  температурної стійкості часових інтервалів у загальному виді відповідно виражаються наступними співвідношеннями:
температурної стійкості часових інтервалів у загальному виді відповідно виражаються наступними співвідношеннями:
 (3)
(3)
 (4)
(4)
де 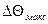 та
та  - відповідно максимальна та мінімальна границя допуску на відхилення часових інтервалів.
- відповідно максимальна та мінімальна границя допуску на відхилення часових інтервалів.
Використовуючи вираз (2) і одночасно міняючи порядок інтегрування, після очевидних перетворень рівнянь (3) і (4) одержуємо:
 (5)
(5)
 (6)
(6)
Вираз у фігурних дужках в (5) являє собою поточне значення 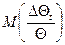 , що було позначено раніше як m(tо). Таким чином, рівняння (5) можна записати у вигляді:
, що було позначено раніше як m(tо). Таким чином, рівняння (5) можна записати у вигляді:
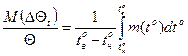 . (7)
. (7)
Аналогічно виразу (5) в виразі (6) у фігурних дужках є значення, яке являє собою поточне значення моменту другого порядку, тобто величину m2(tо)+d2(tо). Маючи це у виді, одержуємо:
 (8)
(8)
З розглянутих виразів (7) і (8) видно, що визначення середнього значення й дисперсії температурної стійкості часових інтервалів, що може очікуватися в заданих умовах експлуатації, по суті зводиться до відшукання функції m(tо) та d(tо), тому що по них без особливих утруднень можуть бути отримані М(∆Θt) і D(∆Θt).
Так, наприклад, для партії ПФС, яка досліджувалась в лабораторії на предмет визначення залежності відносного відхилення часових інтервалів від температури, виконаємо статистичну обробку і представимо функції m(tо) та d(tо) у вигляді вибіркових значень для фіксованих температур tо (-10оС; 0оС; +10оС; +20оС; +30оС; +40оС; +50оС; +60оС; +70оС; +80оС).
Дискретні значення функції m(tо) отримаємо за допомогою формули визначення середньо арифметичного значення:
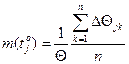 . (9)
. (9)
Відповідно, дискретні значення функції d(tо) отримаємо за допомогою відомої формули для дисперсії, а саме:
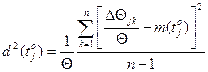 . (10)
. (10)
В формулах (9), (10) індекси мають такі значення: j - дискретне значення температури tо, для якого виконувалась статистична обробка ( 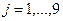 ); k - номер екземпляру ПФС вибіркової партії (
); k - номер екземпляру ПФС вибіркової партії ( 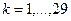 ).
).
Результати статистичної обробки у вигляді дискретних значень функції  та
та 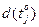 наведені на рис.3 (маркери, відповідно позначені квадратами та кругами).
наведені на рис.3 (маркери, відповідно позначені квадратами та кругами).

Рисунок 3 - Результати статистичної обробки у вигляді функції m(tо) та d(tо)
3.2. Апроксимація нелінійних температурних характеристик вибіркової партії ПФС. Проведені дослідження досить представницької вибіркової партії ПФС дозволили визначити для кожного екземпляра залежність інтервалів часу між періодичними відліками часу від температури. Враховуючи достатньо високу точності настроювання прецизійних генераторів ПФС на номінальне значення частоти та використання прецизійних стабілізаторів напруги живлення сімейство кривих має криві, що перетинаються в точці номінального значення температури, при якій виконується настроювання і розбіжних від її в обидва боки пучки (див. рис.2).
Узагальнені результати досліджень температурної залежності всієї множини ПФС, які наведені на рис.2, результати статистичної обробки (рис.3) температурних характеристик вибіркової партії прецизійних формувачів з кільцем фазового автопідстроювання у вигляді функції  підтверджують факт їх нелінійності.
підтверджують факт їх нелінійності.
В зв'язку з цим, для проведення аналітичного аналізу необхідно формалізувати отримані результати температурної залежності. Виконаємо апроксимацію дискретних значень температурних характеристик вибіркової партії ПФС функції m(tо) гладкою кривою, яка аналітично може бути представлена ступеневим рядом з членами не вище третього порядку:
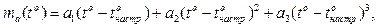 (11)
(11)
де а1, а2, а3 – коефіцієнти, що залежать від характеристик ПФС, а також від вибору величини tнастр – температури, при якій відбувається настроювання ПФС.
Настроювання вибіркової партії ПФС виконувалось в приміщенні, що кондиціонується при температурі tнастр =20оС. Позначимо величиною  різницю
різницю
 . (12)
. (12)
Тоді рівняння (12) перепишеться у вигляді:
 . (13)
. (13)
Коефіцієнти ступеневого ряду (12), (13) залежать від електричних та конструктивних характеристик ПФС. Для визначення цих залежностей, на підставі детальних експериментальних досліджень партії однотипних ВПС, у структурі пристрою виділено групу елементів, функціонально об'єднаних у вузол, названий генератором, що управляється кодом (ГУК) (рис.4). Загальною ознакою виділеної групи є факт їхнього домінуючого внеску в сумарну нестабільність часових інтервалів.
ГУК, структурна схема якого представлена на рис.4, реалізується на стандартній друкованій платі розміром 160х100 мм. Габаритні розміри корпусів генераторів керованих напругою типу ГК-89, ГК-75, ГК-90, що випускають фірмою «МОРИОН» і використовуються як компоненти при виготовленні ГУК, становлять 51х51х38 мм, 51х51х25 мм, 51х51х12,7 мм відповідно. Інші компоненти схеми мають стандартні корпуси, а саме ЦАП фірми «BURR BRAUN» DAC1220 - корпус SSOP-16; ДОН фірми «BURR BRAUN» REF 1004-2,5 - восьмививідний корпус SOIC з монтажними габаритами 10х3,1х1,75 мм; КН - фірми «ANALOG DEVICES» CMP401 - шістнадцятививідний корпус SOIC з монтажними габаритами 10х6,2х1,75 мм. Площа, що будуть займати на платі друкованого монтажу генератор, що управляється напругою й інші компоненти в порівнянні із площею плати дозволяє забезпечити можливість раціонального компонування з урахуванням забезпечення оптимальної температурної стійкості сигналу ПВЧ.
Для цього розташуємо друковану плату, на якій розміщується ГУК, в Декартовій системі координат (див. рис.5). ГУН розташовано в лівій нижній частині, а розташування таких елементів, як ЦАП, ДОН, КН, будемо виконувати в верхній частині плати на відстані L від осі ординат.
  | |||
 | |||
Таке представлення взаємного розташування компонентів ГУК на друкованій платі дає змогу виконати аналітичне дослідження впливу ряду факторів на стійкість синхросигналу, що формується ПФС. Наприклад, якщо вибрати температуру настроювання вибіркової партії ПФС tнастр =20оС то залежність коефіцієнтів а1, а2, а3 рівняння (13) від відстані L може бути достатньо точно представлена формулами:
 (14)
(14)
При цьому будемо виконувати обмеження, щодо розташування групи елементів ЦАП, ДОН, КН в межах плати, а саме  .
.
Користуючись рівнянням (13) з врахуванням значень коефіцієнтів а1, а2, а3 рівняння (14) виконаємо розрахунки апроксимуючої кривої для значень температур від мінус 10оС до плюс 70оС для випадку розташування групи елементів ЦАП, ДОН, КН на відстані  від лінії ординат (рис.5).
від лінії ординат (рис.5).
Спочатку розрахуємо коефіцієнти а1, а2, а3 рівняння (14):
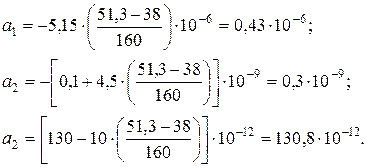 (15)
(15)
Для температури мінус 10оС функція mа(tо) приймає значення:
 (16)
(16)
Результати розрахунків функції mа(tо) для інших значень температури приведені в табл.1 та відповідно цих значень на рис.3 суцільною кривою представлено апроксимуючу функцію дискретних значень функції  , яка отримана на основі експериментальних даних. З аналізу графіка рис.3 можна зробити висновок, що апроксимуюча функція достатньо точно представляє експериментально отримані результати і може в подальшому використовуватись для аналітичних досліджень ПФС екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах.
, яка отримана на основі експериментальних даних. З аналізу графіка рис.3 можна зробити висновок, що апроксимуюча функція достатньо точно представляє експериментально отримані результати і може в подальшому використовуватись для аналітичних досліджень ПФС екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах.
Таблиця 1
Апроксимуюча крива функції 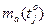
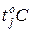
| -10 | ||||||||

| -16,2 | -9,5 | -4,4 | 4,46 | 9,77 | 16,7 | 26,05 | 38,6 |
Виконаємо деякі дослідження залежності 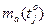 , показаної на рис.3. Неважко бачити, що функція (13) може мати два екстремуми в точках
, показаної на рис.3. Неважко бачити, що функція (13) може мати два екстремуми в точках
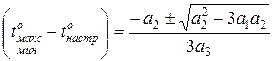 (17)
(17)
і один перегин у точці
 (18)
(18)
При обмеженніінтервалу зміни температури практично можливими межами спостерігаються два види залежностей відхилення часових інтервалів від температури:
- у випадку малої величини а2, коли  , як це слідує з виразу (17), також мала величина, то точка перегину лежить у робочому інтервалі зміни температури й крива має повний вигляд із двома екстремумами;
, як це слідує з виразу (17), також мала величина, то точка перегину лежить у робочому інтервалі зміни температури й крива має повний вигляд із двома екстремумами;
- у випадку щодо великої величини а2, коли  також має великі значення, точка перегину лежить поза робочим інтервалом зміни температури (звичайно лівіше інтервалу), тому в нього входить тільки одна напівхвиля кривої з одним екстремальним значенням, тобто друга напівхвиля тут практичного значення вже не має.
також має великі значення, точка перегину лежить поза робочим інтервалом зміни температури (звичайно лівіше інтервалу), тому в нього входить тільки одна напівхвиля кривої з одним екстремальним значенням, тобто друга напівхвиля тут практичного значення вже не має.
Також можна констатувати, що в більшості випадків коефіцієнт а2 в формулі (14), що другий член рівняння (13) можна не враховувати. При цьому, як слідує з (18) точка перегину автоматично співпадає з точкою настроювання  . Звідси виходить приблизна рівність:
. Звідси виходить приблизна рівність:
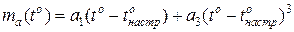 . (19)
. (19)
Для того щоб отримати функцію  , необхідно знайти поточне значення середнього квадратичного відхилення величини
, необхідно знайти поточне значення середнього квадратичного відхилення величини 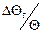 . Якщо тепер врахувати припущення (19), пов’язані з малими величинами, то можна отримати наступний вираз:
. Якщо тепер врахувати припущення (19), пов’язані з малими величинами, то можна отримати наступний вираз:
 (20)
(20)
Або з врахуванням (14)
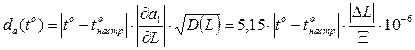 , (21)
, (21)
де  - похибка дискретності розташування на платі елементів;
- похибка дискретності розташування на платі елементів;
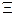 - коефіцієнт, що залежить від характеру похибки дискретності розташування елементів.
- коефіцієнт, що залежить від характеру похибки дискретності розташування елементів.
Якщо припустити, що похибка розташування на платі елементів складає 4 мм, то апроксимуюча функція  може бути записана у вигляді:
може бути записана у вигляді:
 (22)
(22)
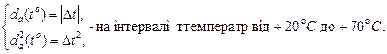 (23)
(23)
Користуючись рівняннями (22) та (23) виконаємо розрахунки апроксимуючої кривої  для значень температур від мінус 10оС до плюс 70оС. Результати розрахунків функції
для значень температур від мінус 10оС до плюс 70оС. Результати розрахунків функції  для заданих значень температури приведені в табл.2 та відповідно цих значень на рис.3 суцільною кривою представлено апроксимуючу функцію дискретних значень функції
для заданих значень температури приведені в табл.2 та відповідно цих значень на рис.3 суцільною кривою представлено апроксимуючу функцію дискретних значень функції 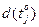 , яка отримана на основі експериментальних даних. З аналізу графіка рис.3 можна зробити висновок, що апроксимуюча функція достатньо точно представляє експериментально отримані результати і може в подальшому використовуватись для аналітичних досліджень ПФС екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах.
, яка отримана на основі експериментальних даних. З аналізу графіка рис.3 можна зробити висновок, що апроксимуюча функція достатньо точно представляє експериментально отримані результати і може в подальшому використовуватись для аналітичних досліджень ПФС екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах.
Таблиця 2
Апроксимуюча крива функції 
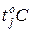
| -10 | ||||||||
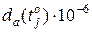
| 23,1 | 15,4 | 7,7 |
3.3. Дисперсія та середнє значення температурної стійкості інтервалів часу. На основі отриманих значень апроксимуючої функції  з врахуванням рівняння (7) середнє значення М(∆Θt) температурної стійкості інтервалів часу може бути виражено формулою:
з врахуванням рівняння (7) середнє значення М(∆Θt) температурної стійкості інтервалів часу може бути виражено формулою:
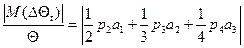 ,(24)
,(24)
де коефіцієнти рn визначаються з рівняння:
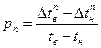 , (25)
, (25)
в якому відповідно позначені інтервали нагріву та охолодження відносно температури настройки tнастр:
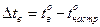 ,
, 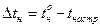 . (26)
. (26)
Оскільки в виразу (25) коефіцієнти рn цілком визначаються заданими умовами зміни температури відповідно до формул (26), то змінними залишаються тільки коефіцієнти а1, а2, а3, які при заданій tнастр визначаються орієнтацією на друкованій платі згрупованих елементів (ЦАП, ДОН, КН), зображених на рис.5.
Аналогічно на основі отриманих значень апроксимуючої функції  та апроксимуючої функції
та апроксимуючої функції 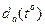 з врахуванням рівняння (8) отримаємо формулу для визначення дисперсії D(∆Θt) температурної стійкості інтервалів часу між ПВЧ.
з врахуванням рівняння (8) отримаємо формулу для визначення дисперсії D(∆Θt) температурної стійкості інтервалів часу між ПВЧ.
Складова 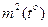 рівняння (8) визначається формулою:
рівняння (8) визначається формулою:
 . (27)
. (27)
Якщо врахувати те, що величина  згідно (21) має наступну залежність
згідно (21) має наступну залежність
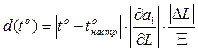 , (28)
, (28)
то складова 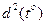 рівняння (8) визначається формулою:
рівняння (8) визначається формулою:
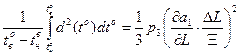 . (29)
. (29)
Підстановка в рівняння (8) отриманих значень для їх складових дає:
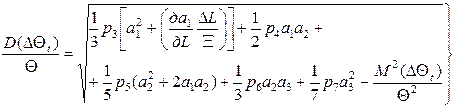 ,(30)
,(30)
Таким чином, формули (24) і (30) дають можливість обчислити середнє значення й дисперсію температурної стійкості частоти партії однотипних пристроїв ПФС у реальних умовах експлуатації. Дані про умови експлуатації входять у формули у вигляді коефіцієнтів pn, які залежать від граничних значень температури і температури настройки.
Читайте також:
- ABC-XYZ аналіз
- I етап. Аналіз впливу типів ринку на цінову політику.
- I. Аналіз контрольної роботи.
- II. Багатофакторний дискримінантний аналіз.
- III етап. Аналіз факторів, що визначають цінову політику підприємства.
- IІI розділ. Аналіз стану маркетингового середовища підприємства
- SWOT-аналіз у туризмі
- SWOT-аналіз.
- Tема 4. Фації та формації в історико-геологічному аналізі
- V. Нюховий аналізатор
- VI етап. Аналіз варіантів зміни цін конкурентами.
- VI. Виконайте граматичний аналіз підкреслених речень.
| <== попередня сторінка | | | наступна сторінка ==> |
| Аналіз умов технічної експлуатації територіально розподілених ПФС екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних | | | Визначення статистичного критерію оптимізації температурної стійкості ПФС |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |