• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення статистичного критерію оптимізації температурної стійкості ПФС

Температурна складова стабільності часових інтервалів ПФС є функцією багатьох змінних, частина з яких доступна для підбору, для того, щоб домогтися по можливості найкращого значення температурної стійкості. Відомо, що для випадкових функцій немає єдиного критерію екстремальності, він повинен вибиратися залежно від конкретних умов [2, 3]. Ця обставина змушує вибрати найбільш підходящий критерій, по якому можна було б судити про максимальні значення температурної стійкості часових інтервалів . Крім того, цей критерій досить корисний для обґрунтованого порівняння різних пристроїв або різних умов експлуатації по такому найважливішому показнику, як температурна стійкість часових інтервалів.

На підставі вище викладеного можна зробити висновок, що критерієм для оцінки температурної нестійкості часових інтервалів безлічі однотипних ПФС можна вважати тільки границі допуску на сумарну нестабільність часових інтервалів.

У випадку, коли здійснюється взаємодія із різними територіально розподіленими ПФС, характеристики нестабільності часових інтервалів, яких заздалегідь невідомі, а відомі тільки дані тільки про сумарну нестабільність часових інтервалів ПФС, то можна за критерій температурної стійкості часових інтервалів можна вважати сумарну нестабільність часових інтервалів. Отже, у всіх випадках критерієм буде величина сумарної нестабільність часових інтервалів:

(31)

Безпосереднє користування таким критерієм дуже незручно, тому що необхідно щораз робити досить складні розрахунки середніх значень, а головне дисперсії всієї складової сумарної нестабільності часових інтервалів , для чого не завжди є потрібні дані.

Виходом з цієї ситуації може бути припущення того, що дисперсія температурної складової не повинна домінувати в сумарній дисперсії. Якщо дисперсія не перевищує половини сумарної дисперсії, тобто 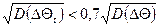, то, можна застосовуючи відому формулу наближених обчислень [2]. А саме, з точністю не гірше 4% вираз (31) можна представити у вигляді:

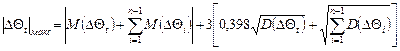(32)

або

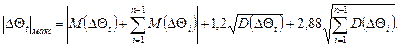(33)

Більш детально розглянемо складові виразу (33), а саме величину, яку назвемо джэй-параметром:

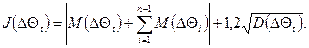(34)

Часто сума середніх значень інших складових нестабільності часових інтервалів дорівнює нулю. У такому випадку критерій оцінки - джэй-параметр температурної стійкості часових інтервалів приймає досить простий вид

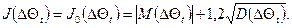(35)

При змінах М(∆Θt) і D(∆Θt) джэй-параметр із достатньою точністю буде відображати вплив температурної складової на сумарну нестабільність часових інтервалів. Із цього погляду джэй-параметр має явні переваги перед математичним очікуванням М(∆Θt), моментом другого порядку або допуском для оцінки величини ∆Θt .

Читайте також:

1. CMM. Визначення моделі зрілості.
2. I визначення впливу окремих факторів
3. I. Постановка завдання статистичного дослідження
4. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
5. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
6. III. Економічна інтерпретація результатів статистичного дослідження банків
7. Ocнoвнi визначення здоров'я
8. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
9. А. Визначення розмірів і площі зони хімічного зараження.
10. Абсолютні показники фінансової стійкості
11. Абсолютні показники фінансової стійкості та її типи
12. Алгебраїчний спосіб визначення точки беззбитковості

Переглядів: 621