• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Епюр точки

Епюр точки (її плоский рисунок) одержують суміщенням горизонтальної П₁ та фронтальної П₂ площин проекцій відносно осі Ζ, тобто обертанням горизонтальної П₁ та профільної П₃ площин проекцій навколо їх ліній перетину Х та Ζ в одну площину, яка суміщається з фронтальною площиною проекцій. При суміщенні вказаних площин площини проекцій П₁ та П₃ роз’єднані вздовж осі Υ. Тому надалі під позначенням осі Υ будемо розуміти відповідно Υ₁(як та, що належить П₁) та Υ₃(як та, що належить П₃). Епюр, плоский рисунок, може складатись з двох або трьох ортогональних проекцій.

Рисунок 1 – Положення точок в октантах

Винесемо І октант та утворимо епюр (рис. 2, а, б).

Надалі будемо використовувати такі умовні позначення та назви:

А₁ – горизонтальна проекція точки А;

А₂ – фронтальна проекція точки А;

А₃ – профільна проекція точки А.

Кожна із проекцій точок будується на перетині горизонтальних та вертикальних ліній, які обмежують відповідні координати Х, Υ, Ζ заданої точки. Тому відповідні проекції, наприклад т. А, можна символьно записати такими визначниками: А₁(х, y), А₂(х, z), А₃(y, z). Лінії А₁А₂ та А₂А₃ називаються, відповідно, вертикальною та горизонтальною лініями зв’язку.

Винесемо ІІ октант та побудуємо епюр точки В (рис. 3, а, б, в).

Винесемо ІV октант та покажемо епюр точки D (рис. 4, а, б, в).

Примітка: Для закріплення цієї теми студенту пропонується здійснити аналогічні побудови стосовно винесення ІІІ октанта та побудови в цьому октанті трьох проекцій точки С. Координати точки С вибираються довільно.

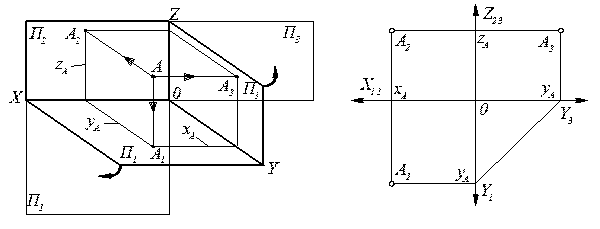
а) просторове зображення т. А б) епюр т. А

та суміщення площин проекцій

Рисунок 2 – Утворення епюра т. А

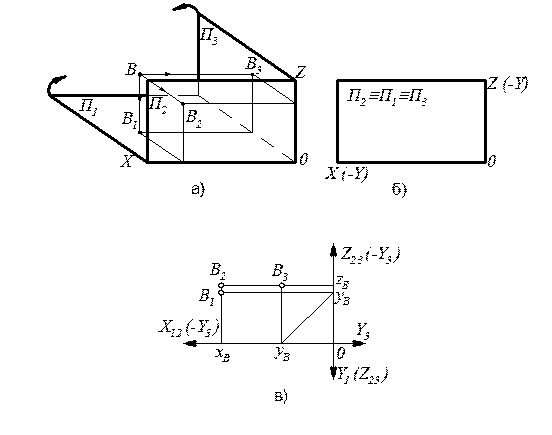
а) просторове зображення б) суміщення площин в)епюр т. В

т. В проекцій

Рисунок 3 – Утворення епюра т. В

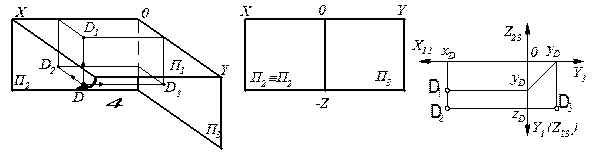
а) просторове зображення б) суміщення площин в) епюр т. D

т. D проекцій

Рисунок 4 – Утворення епюра т. D

Крім цього, точки можуть знаходитись в площинах проекцій або на осях. Точка належить одній із площин проекцій, якщо у неї відсутня одна із координат.

Якщо абсциса точки х=0, то точка належить П₁; ордината у=0, то точка належить П₂; апліката z=0, то точка належить П₃. Наприклад, якщо точка Е належить площині проекцій П₂ (Е є П₂), то умовний запис визначника такий: Е (х, 0 , z).

Точка належить одній із координатних осей, якщо у неї відсутні дві координати. Якщо у точки координати у,z=0, то точка належить осі абсцис х; якщо у точки координати х,z=0, то точка належить осі ординат у; якщо у точки координати х,у=0, то точка належить осі аплікат z.

Тобто, згідно з умовою запису визначника для т. F (0, 0, 20), слід розуміти, що точка F належить осі аплікат z і знаходиться на відстані 20мм від початку координат.

Якщо розглядати в просторі декілька точок, то за взаємним положенням вони можуть бути рівновіддалені від певної площини проекцій. Згідно з трьома координатами будь-якої точки абсциса X характеризує віддаленість від площини проекцій П₃, ордината У – від П₂, апліката z – від П₁. Наприклад, т. М та N рівновіддалені від П₃, значить їх аплікати Z за модулем характеризуються однаковими числовими значеннями, тобто |Z_M|=|Z_N|. Точки, S та Q, які рівновіддалені від П₂, мають однакові ординати |Y_S|=|Y_Q|, аналогічно, якщо |Х_Е|=|Х_F|, то т. Е та т. F рівновіддалені від П_3.

Читайте також:

1. Алгебраїчний спосіб визначення точки беззбитковості
2. Аналіз точки беззбитковості
3. Антропометричні точки
4. В положение ее в данной момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется переменками.
5. Валентність з точки зору будови атома.
6. Вибір прицілу, точки прицілювання та цілика
7. Видалення характерної точки
8. Визначення прямокутних зональних координат X та Y точки N на карті
9. Визначення точки
10. Визначення точки беззбитковості
11. Визначення точки беззбитковості
12. Визначення точки беззбитковості виробництва

Переглядів: 3402