• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поверхні обертання

Умовний запис визначника поверхонь – W (l, і) (рис.62),

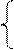
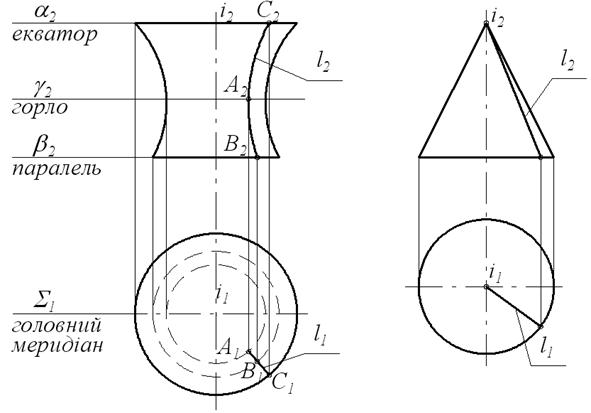
а) l – плоска крива б) l – пряма лінія

Рисунок 62 – Утворення поверхонь обертання

Поверхні обертання можна отримати, якщо деяку твірну l, обертати навколо oсі i, причому в якості твірної може бути пряма, плоска або просторова крива (рис. 62, а, б).На поверхні обертання найпростішою лінією є коло. Кола отримуємо, якщо поверхню перетнути площинами, які

перпендикулярні до осі обертання поверхні, і надалі будемо їх називати паралелями (здобуті площиною β).

Паралель найменшого радіуса, здобута площиною γ, називається

горлом. Паралель найбільшого радіуса, здобута площиною α, називається екватором.

Лінія, здобута перерізом поверхні площиною, яка проходить через вісь обертання і, називається меридіаном.

Головний меридіан – меридіан, який знаходиться в площині, що

паралельна одній з площин проекцій (здобута площиною Σ). Головний меридіан утворює обрис поверхні та дозволяє визначати видимість поверхні.

Поверхні обертання з плоскою твірною другого порядку мають назву меридіана, аналогічну назві цієї твірної (для параболоїда обертання – парабола, еліпсоїда – еліпс, і т.д.) Ці поверхні відносять до закономірних.

Читайте також:

1. Ne і ne – поточне значення потужності і частоти обертання колінчастого вала.
2. Алгоритм визначення проекцій точок на поверхнях обертання
3. Алгоритм розрахунку температури поверхні чипу ІМС процесора
4. Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
5. В'язкості і тиску повітря від профілю тіла, стану його поверхні і положення тіла в повітряному потоці.
6. Великої питомої поверхні пилинок (відношення площі поверхні до їх
7. Взаємний перетин поверхонь тіл обертання
8. ВИЗНАЧЕННЯ МІНІМАЛЬНОГО ЗНАЧЕННЯ ТЕМПЕРАТУРИ НА ВНУТРІШНІЙ ПОВЕРХНІ
9. Визначення напруг на похилих площадках. Умови на поверхні
10. Визначення температури на поверхні ізоляції принадземномупрокладанні та при прокладанні трубопроводів в приміщенні.
11. ВИЗНАЧЕННЯ ТЕМПЕРАТУРНОГО ПЕРЕПАДУ МІЖ ТЕМПЕРАТУРОЮ ВНУТРІШНЬОГО ПОВІТРЯ І ПРИВЕДЕНОЮ ТЕМПЕРАТУРОЮ ВНУТРІШНІЙ ПОВЕРХНІ
12. Визначення центру обертання провідної ланки або другий наслідок основної теореми зачеплення.

Переглядів: 895