• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Окремі випадки перетину

1. Поверхні, які перетинаються, мають спільну вісь обертання і

(рис. 96).

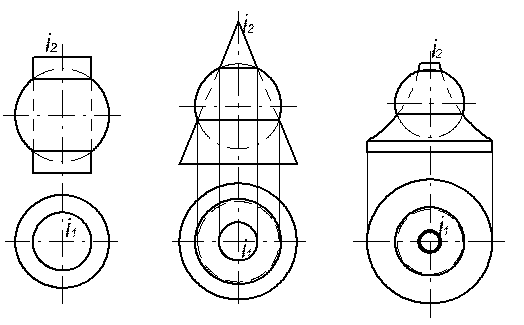
а) б) в)

Рисунок 96 – Співвісні поверхні

На рис. 96 показані 3 приклади: а) циліндр та сфера, б) конус та сфера, в) поверхня обертання та сфера. Лінією перетину є коло (паралель). Приклади зображень співвісних поверхонь обертання, що мають застосування в машинобудівельному кресленні, показані на рис. 97. Поверхні позначені буквами: Кн. – конус, Ц – циліндр, Сф – сфера. Отримана лінія перетину позначена буквою Ко – коло.

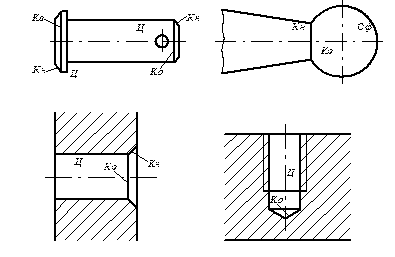
Рисунок 97 – Приклади зображень співвісних поверхонь із практики машинобудівельних креслень

2. Поверхні обертання, які описані навколо спільної для них сфери (рис. 98).

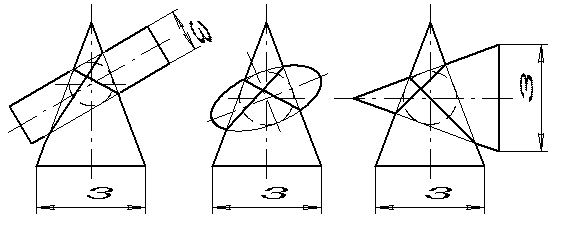
Рисунок 98 – Поверхні, які перетинаються, описані навколо спільної сфери

Цей випадок перетину підпорядкований відомій теоремі Монжа: дві поверхні другого порядку, які описані навколо третьої поверхні другого порядку (сфери), перетинаються між собою по двох кривим другого порядку. Дійсно, згідно рис. 98, перетинаються поверхні обертання: циліндр і конус, еліпсоїд і конус, два конуси. Лініями перетину вказаних поверхонь будуть еліпси.

3. Одна із поверхонь займає проекціювальне положення (рис. 99).

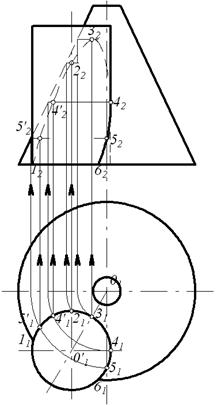
Рисунок 99 – Бічна поверхня циліндра займає проекціювальне положення

Вихідна проекція шуканої лінії перетину збігається з виродженою проекцією проекціювальної поверхні. Друга проекція лінії взаємного перетину визначається за її належністю поверхні загального положення. До характерних точок в даному випадку відносять такі: 1, 6 – найнижчі, 3 – найвища, 4 – та, що визначає видимість поверхонь. Точки 2, 5 є проміжними. Фронтальні проекції точок 1, 6 визначаються безпосередньо (належать основам конуса та циліндра), інші фронтальні проекції точок 2, 3, 4, 5 знаходять за допомогою паралелей на конусі. Видимою частиною є лінія перетину, що складається із точок 6, 5, 4; решту з’єднують невидимим контуром.

Читайте також:

1. Акти за формою Н – 5, Н – 1 та НПВ. Нещасні випадки пов’язані з виробництвом і не пов’язані з виробництвом.
2. Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
3. Банк даних про випадки порушень статутних правил взаємовідносин у військовому підрозділі
4. Вибір форми перетину гірничої виробки та вигляду крепі.
5. Види злочинів. Відповідальність за окремі злочини
6. Визначення площі поперечного перетину відкотної виробки в світлі.
7. Випадки множення і ділення в межах 1000, які зводяться до табличних. Розв'язання задач.
8. Випадки проведення та обмеження щодо проведення оцінки майна
9. Випадки, коли приймається рішення про фінансову санацію підприємств
10. Виробничі травми, профзахворювання, нещасні випадки виробничого характеру.
11. Виробничі функції - два особливих випадки
12. Відповідальність за окремі види злочинів.

Переглядів: 768