• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Сутність ММП полягає в тому, що за якісну оцінку параметра а беруть таке значення аргументу, що приводить функцію L до максимуму. Рівняння (4.14) розв’язують при умові

. (4.15)

При цьому вибирають таке визначення а, яке зводить функцію L до максимуму. Для спрощення функцію правдоподібності заміняють логарифмом, тоді

. (4.16)

Якщо закон розподілу має два параметри: а₁і а₂, то оцінки їх визначають із сумісного розв’язання двох рівнянь

і 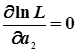. (4.17)

Приклад 1. При експериментальних випробуваннях точності розробленого приладу отримана вибірка із генеральної сукупності x₁,x₂,…,x_n. Результати вимірів х_і незалежні між собою. Попередні розрахунки показали, що статистична функція (гістограма) має вигляд щільності нормального розподілу. Необхідно знайти оцінку для невідомого параметра а = М_Х, що відображає ймовірне значення шуканої величини Х.

Розв’язання. Так як результати експерименту підпорядковуються нормальному закону розподілу, то висунемо умову, що щільність розподілу кожної із величин j (х_і, а) залежить від параметра а. Це означає, що для кожної величини функції правдоподібності буде

.

Тоді функція правдоподібності для всієї вибірки буде

L(x₁ ,x₂,…,x_n, a ) = .

Візьмемо логарифм, тоді

.

За допомогою формули (4.16) отримаємо

.

При цьому необхідно щоб s² ¹ 0, тоді

, або .

Оцінкою невідомого параметру а буде

. (4.18)

Таким чином надійним значенням параметра а буде проста арифметична середина 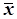із результатів експерименту.

Приклад 2. Згідно умов приклада 1 результати вибірки підпорядковуються закону нормального розподілу. Необхідно визначити оцінки а₁ = М_Х, а₂ = s²,що характеризують величину і дисперсію вибірки.

Розв’язання. Згідно формули щільності закону нормального розподілу з параметрами а₁ = М_Х і а₂ = s²для кожної випадкової величини х_і функція правдоподібності буде

,

а для всієї вибірки

.

Згідно формули (4.17) отримаємо два рівняння і прирівняємо їх до нуля

;

,

або

; а)

(4.19)

. б)

Із сумісного їх розв’язання отримаємо

; (4.20)

. (4.21)

Як видно, що перший параметр буде простою арифметичною серединою 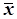(формула 4.18), а другий параметр буде статистичною дисперсією (§ 4.4).

Проте виявляється, що при невідомому значенні істинного (ймовірного) значення шуканої випадкової величини Х оцінка дисперсії буде дещо зміщеною. Тому при заміні математичного сподівання М_Х простою арифметичною серединою 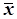незміщеною оцінкою дисперсії буде

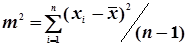. (4.22)

В математичній обробці результатів вимірів вираз (4.21) називають формулою Гаусса, а (4.22) – формулою Бесcеля.

Метод максимальної правдоподібності приводить до визначення досить доброякісних оцінок, хоч іноді і зміщених. Проте практично можуть виникати досить складні системи рівнянь.

Читайте також:

1. CMM. Визначення моделі зрілості.
2. DIMCLRE (РЗМЦВЛ) - колір виносних ліній (номер кольору). Може приймати значенняBYBLOCK (ПОБЛОКУ) і BYLAYER (ПОСЛОЮ).
3. I визначення впливу окремих факторів
4. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
5. I. Органи і системи, що забезпечують функцію виділення
6. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
7. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
8. II. Фактори, що впливають на зарплату при зарубіжних призначеннях
9. ISO 15504. Призначення і структура стандарту
10. Iсторичне значення революції.
11. Ne і ne – поточне значення потужності і частоти обертання колінчастого вала.
12. Ocнoвнi визначення здоров'я

Переглядів: 422