
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Числові характеристики статистичного розподілу
Закон розподілу випадкової величини Х характеризує її з ймовірної точки зору. Між тим при вирішенні багатьох практичних задач достатньо знати тільки окремі її числові характеристики, що відображають найбільш істотні риси розподілу випадкової величини.
Ми уже познайомилися з основними числовими характеристиками випадкових величин: математичним сподіванням, дисперсією, початковими та центральними моментами, асиметрією та ексцесом.
Для статистичного розподілу існують такі ж самі числові характеристики. Справа зводиться до того, щоб по результатам експериментів знайти формули їх обчислень.
Так аналогічно для математичного сподівання випадкової величини Х є середнє арифметичне результатів спостережень 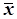 випадкової величини біля якого ґрунтуються її можливі значення
випадкової величини біля якого ґрунтуються її можливі значення
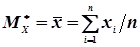 , (4.23)
, (4.23)
де хі – значення випадкової величини в кожному і-ому досліді;
n – кількість дослідів.
Величину 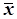 називають статистичним середнім випадкової величини Х. Слід зазначити, що при досить великій кількості дослідів п статистичне середнє
називають статистичним середнім випадкової величини Х. Слід зазначити, що при досить великій кількості дослідів п статистичне середнє 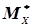 або
або 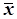 наближається до математичного сподівання випадкової величини Х і може бути прийнятим замість нього, тобто
наближається до математичного сподівання випадкової величини Х і може бути прийнятим замість нього, тобто
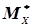 =
= 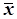 » МХ.
» МХ.
Аналогією дисперсії випадкової величини Х є статистична дисперсія, що обчислюється за формулою
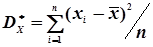 . (4.24)
. (4.24)
В методі моментів обчислюють статистичні початкові та центральні моменти будь-якого порядку за формулами
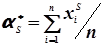 ; (4.25)
; (4.25)
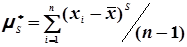 . (4.26)
. (4.26)
Для статистичного ряду розбитого на групи, тобто для статистичної сукупності маємо
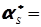
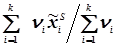 ; (4.27)
; (4.27)
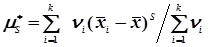 , (4.28)
, (4.28)
де nі - кількість результатів в і-ій групі;
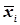 - статистичне середнє і-ої групи;
- статистичне середнє і-ої групи;
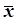 - загальне статистичне середнє.
- загальне статистичне середнє.
Аналіз формул (4.20), (4.21) і (4.22) показує, що середнє арифметичне 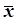 » МХ, а статистична дисперсія m2 » DX, тобто вони будуть найбільш вірогідними оцінками параметрів закону нормального розподілу.
» МХ, а статистична дисперсія m2 » DX, тобто вони будуть найбільш вірогідними оцінками параметрів закону нормального розподілу.
Слід зазначити, що при виведенні формул в ММП передбачали, що результати експерименту незалежні і проводились в однакових умовах. Тобто комплекс умов: об’єкт, суб’єкт, прилад, зовнішнє середовище і метод вимірювання були незмінними. Такі виміри називають рівноточними. При цьому дисперсії окремих вимірів будуть однаковими, тобто 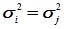 або
або 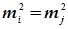 .
.
Це дозволяє нам стверджувати, що при рівноточних вимірах найближчим значенням вимірюваної величини є середнє арифметичне 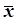 (формула 4.20), а значенням дисперсії буде
(формула 4.20), а значенням дисперсії буде 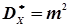 (формули 4.21 та 4.22).
(формули 4.21 та 4.22).
Проте на практиці не завжди можна зберегти незмінність комплексу умов. Тоді кожен результат експерименту буде дещо відрізнятися по точності і кожній випадковій величині 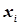 буде відповідати своя дисперсія
буде відповідати своя дисперсія 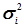 , тобто статистичний ряд буде мати вигляд
, тобто статистичний ряд буде мати вигляд
х1, х2, ... , хп,
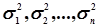 . (4.29)
. (4.29)
Такі виміри, коли дисперсії 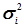 ¹
¹ 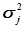 , називають нерівноточними.
, називають нерівноточними.
Для визначення приблизних значень вимірюваної величини та дисперсії при нерівноточних вимірах, виходячи з того, що 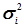 ¹
¹ 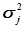 , систему рівнянь (4.19) запишемо у вигляді
, систему рівнянь (4.19) запишемо у вигляді
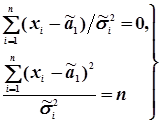 . (4.30)
. (4.30)
В теорії математичної обробки при нерівноточних вимірах вводять поняття ваги, тобто
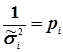 , (4.31)
, (4.31)
де рі - вага виміру, або вага випадкової величини хі. Тоді статистичний ряд (4.29) можна переписати в вигляді
х1, х2, ... , хп,
р1, р2, ... , рп.(4.32)
Вага рі буде характеризувати міру відносної точності результатів експериментів. При цьому їх можна збільшувати, чи зменшувати на однакове число С. Тоді формула (4.31) буде
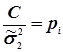 . (4.33)
. (4.33)
Для спрощення вводять поняття середнього квадратичного відхилення одиниці ваги - 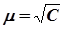 . Тоді вага буде обчислюватися за формулою
. Тоді вага буде обчислюватися за формулою
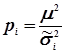 , (4.34)
, (4.34)
а систему рівнянь (4.30) можна переписати у вигляді
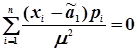 ;
;
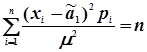 .
.
Із їх сумісного розв’язання знаходять формули обчислення загальної арифметичної середини 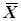 і середнього квадратичного відхилення одиниці ваги
і середнього квадратичного відхилення одиниці ваги
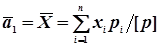 ; (4.35)
; (4.35)
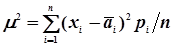 . (4.36)
. (4.36)
Очевидно оцінка дисперсії одиниці ваги m2 » Dxбуде зміщеною. По аналогії з формулою (4.22) незміщеною оцінкою дисперсії одиниці ваги при нерівноточних вимірах буде
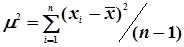 . (4.37)
. (4.37)
Статистичною оцінкою стандарту або середнього квадратичного відхилення sбуде середня квадратична похибка
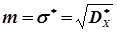 . (4.38)
. (4.38)
При відомому істинному значенню визначуваної величини а її обчислюють за формулою Гаусса
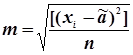 . (4.39)
. (4.39)
Якщо істинне значення визначуваної величини невідоме, то застосовують формулу Бесселя
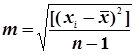 , (4.40)
, (4.40)
де 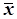 - середнє арифметичне;
- середнє арифметичне;
п – число результатів експерименту.
Додатковими статистичними характеристиками нормального закону розподілу є асиметріята ексцес.
Асиметрія являє собою нормований центральний момент третього порядку, тобто
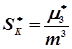 . (4.41)
. (4.41)
Ексцес є мірою крутизни і визначається по формулі
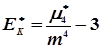 ,(4.42)
,(4.42)
де 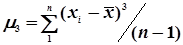 ;
; 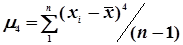 .
.
Приклад 1. В таблиці 4.3 приведені результати експерименту при дослідженні випадкової величини Х. Визначити числові характеристики статистичного розподілу: 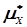 ,
, 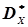 ,
,  і
і 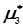 .
.
Таблиця 4.3
| пі | |||||||
| хі | -10 | -2 | +4 | -1 | +4 | +12 | +9 |
Розв’язання. По формулам (4.10) – (4.13) отримаємо
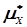 =
= 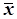 = (-10 –2 + 4 –1 + 4 + 12 + 9) / 7 = + 2;
= (-10 –2 + 4 –1 + 4 + 12 + 9) / 7 = + 2;
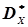 = {(-10-2)2 + (-2 +2)2 + (4 – 2)2 + (-1 –2)2 + (4 – 2)2 + (12 – 2)2 + + (9-2)2} / 7 = 310/7 = 44,3;
= {(-10-2)2 + (-2 +2)2 + (4 – 2)2 + (-1 –2)2 + (4 – 2)2 + (12 – 2)2 + + (9-2)2} / 7 = 310/7 = 44,3;
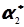 = {(-10)2 + (-2)2 + 42 + (-1)2 + 42 + 122 + 92 } / 7 = 51,7;
= {(-10)2 + (-2)2 + 42 + (-1)2 + 42 + 122 + 92 } / 7 = 51,7;
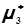 = {(-12)3 + 03 + 23 + (-3)3 + 23 + 103 + 73} / 7 = 444,9.
= {(-12)3 + 03 + 23 + (-3)3 + 23 + 103 + 73} / 7 = 444,9.
Приклад 2. Із статистичного ряду отримано статистичну сукупність (табл..4.4, рядки 1-7). Обчислити статистичний початковий момент першого порядку 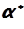 та дисперсію другого порядку
та дисперсію другого порядку 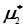 .
.
Таблиця 4.4
 1 1
| № групи | S | |||||||
| Граничні значення | от | -10 | -5 | ||||||
| до | -5 | +5 | |||||||
| Частота nі | |||||||||
Середні 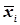
| -7,5 | -2.5 | +2,5 | +7,5 | +12,5 | +17,5 | |||
nі 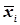
| -15 | -17,5 | +27,5 | +105,0 | 62,5 | 17,5 | |||
( 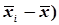
| -12 | -7 | -2 | +3 | +8 | +13 | |||
nі ( 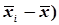 2 2
|
Розв’язання. В рядку 5 визначають загальне середнє статичне. Якщо 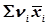 = 180, то за формулою (4.14) обчислюємо:
= 180, то за формулою (4.14) обчислюємо:
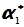 =
= 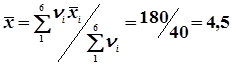 .
.
Потім обчислюють відхилення середніх групи 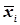 від загального середнього статистичного
від загального середнього статистичного 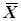 .
. 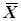 = 4.5. В рядку 7 обчислюють
= 4.5. В рядку 7 обчислюють 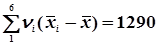 . Тоді статистична дисперсія буде дорівнювати
. Тоді статистична дисперсія буде дорівнювати 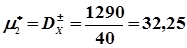 .
.
Для системи двох випадкових величин(х,у)
Числові характеристики визначають за результатами п-незалежних дослідів, які виконують в однакових умовах по значенням:
Х ® х1, х2, ..., хп;
Y ® y1, y2, … , yn.
В свою чергу системи випадкових величин (хі, уі) незалежні, а математичні сподівання, дисперсії і кореляційні моменти будуть однакові, тобто
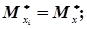
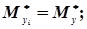
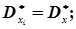

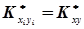 .
.
Виходячи з того, що випадкові величини х і у та система (Х,Y)підкоряються нормальному закону розподілу, а математичні очікування 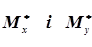 та дисперсії
та дисперсії 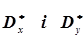 є характеристиками окремих випадкових величин Х і Y із системи (Х, Y),то згідно формул (4.20) і (4.22) маємо
є характеристиками окремих випадкових величин Х і Y із системи (Х, Y),то згідно формул (4.20) і (4.22) маємо
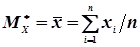 ; (4.43)
; (4.43)
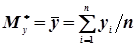 ; (4.44)
; (4.44)
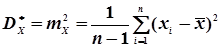 ; (4.45)
; (4.45)
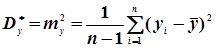 (4.46)
(4.46)
Незміщена та обґрунтована оцінка кореляційного моменту 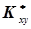 системи випадкових величин (х,у) визначається за формулою
системи випадкових величин (х,у) визначається за формулою
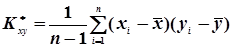 . (4.47)
. (4.47)
Статистичний коефіцієнт кореляції 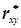 обчислюють за формулою
обчислюють за формулою
 , (4.48)
, (4.48)
де mx та my обчислюють за формулами
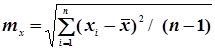 ; (4.49)
; (4.49)
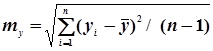 . (4.50)
. (4.50)
Коефіцієнт кореляції 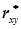 знаходиться в межах
знаходиться в межах
-1 £ 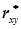 £ +1.
£ +1.
Якщо коефіцієнт кореляції близький до ±1, то між випадковими величинами існує прямолінійний зв’язок. Рівняння регресії визначають за формулами
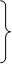 |
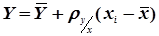 ,
,
або 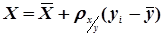 (4.51)
(4.51)
де 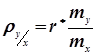 ;
; 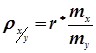 - коефіцієнти регресії.
- коефіцієнти регресії.
Приклад 3. Коефіцієнт Кі нитяного віддалеміра визначався на різних відстанях Dі від точки установки приладу. Обчислити числові характеристики системи випадкових величин (D,К):математичні сподівання, дисперсії та коефіцієнт кореляції. Результати експерименту наведені в табл. 4.5
Таблиця 4.5
| Д(м) | ||||||||
| К | 99.0 | 98.5 | 99.5 | 99.0 | 99.5 | 99.6 | 101.0 | 99.9 |
Розв’язання. Для наочності обчислення зведемо в табл.4.6
Таблиця 4.6
D визначено в сотнях метрів
| № п/п | D | K | Di - 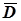
| Ki - 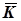
| (Di - 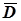 )2 )2
| (Ki- 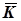 )2 )2
| (Di- 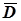 )(Ki - )(Ki - 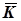 ) )
|
| 0,2 | 99,0 | -0,7 | -0,5 | 0,49 | 0,25 | +0,35 | |
| 0,4 | 98,5 | -0,5 | -1,0 | 0,25 | 1,00 | +0,50 | |
| 0,6 | 99,5 | -0,3 | 0,09 | ||||
| 0,8 | 99,0 | -0,1 | -0,5 | 0,01 | 0,25 | +0,05 | |
| 1,0 | 99,5 | +0,1 | 0,01 | ||||
| 1,2 | 99,6 | +0,3 | +0,1 | 0,09 | 0,01 | +0,03 | |
| 1,4 | 101,0 | +0,5 | +1,5 | 0,25 | 2,25 | +0,75 | |
| 1,6 | 99,9 | +0,7 | +0,4 | 0,49 | 0,16 | +0,28 | |
| S | 1,58 | 3,92 | +1,96 |
Спочатку по формулами (4.43) і (4.44) обчислюють середні арифметичні 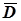 і
і 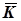
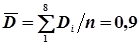 ;
; 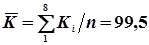 .
.
В графах 3 і 4 таблиці 4.5 обчислюють відхилення Di і Кі від середніх арифметичних 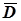 і
і 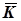 .
.
Контроль: суми відхилень повинні дорівнювати нулю, або величині, що обумовлена помилкою закруглення середніх 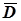 і
і 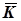 .
.
Далі в графах 5 і 6 обчислюють квадрати відхилень і їх суми: 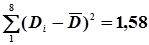 та
та 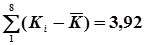 . Це дозволяє за формулами (4.45) і (4.46) визначити дисперсії
. Це дозволяє за формулами (4.45) і (4.46) визначити дисперсії 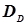 і
і 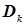 та за формулами (4.49), (4.50) статистичні стандарти mD і mk
та за формулами (4.49), (4.50) статистичні стандарти mD і mk
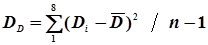 =
= 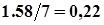 ;
; 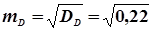 = 0,46;
= 0,46;
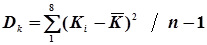 =
= 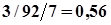 ;
; 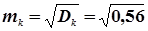 = 0,75.
= 0,75.
По формулі (4.47) обчислюємо кореляційний момент, а по формулі (4.48) коефіцієнт кореляції
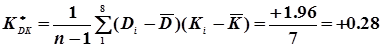 ;
;
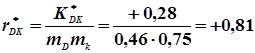 .
.
Так як r* = 0,81, що досить близько до 1, то можна передбачити, що між величинами D і K існує прямолінійний зв’язок. Спочатку обчислимо коефіцієнт регресії
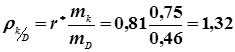 .
.
По формулі (4.37) рівняння регресії К по D буде
К = 99,5 + 1,32 D - 1,32 × 0,9 ,
або К = 1,32 D + 98,31.
По результатам обчислень можна побудувати графік регресії (рис.4.4)
 |
Рис.4.4
Для побудови прямої регресії обчислено значення двох точок К1 = 98,31 при D = 0м і К2 = 99,5 при D = 100м, які наносимо на графік і проводимо через них пряму лінію.
Такий спосіб визначення оцінок невідомих параметрів називають точковим, а самі оцінки – точковими. Його недоліками є те, що точкова оцінка 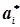 не збігається з величиною аі.Це особливо видно при невеликій кількості результатів експерименту. До цього для визначення точності точкової оцінки слід знати і дисперсію
не збігається з величиною аі.Це особливо видно при невеликій кількості результатів експерименту. До цього для визначення точності точкової оцінки слід знати і дисперсію 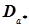
Читайте також:
- I. Доповнення до параграфу про точкову оцінку параметрів розподілу
- I. Постановка завдання статистичного дослідження
- III. Економічна інтерпретація результатів статистичного дослідження банків
- V. Поняття та ознаки (характеристики) злочинності
- VII розділ. Маркетингові рішення з розподілу та збуту товару
- Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
- Автоматизація водорозподілу з комбінованим регулюванням
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Автоматизація водорозподілу регулювання зі сталими перепадами
- Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
- Автоматизація водорозподілу регулюванням за верхнім б'єфом
- Автоматизація водорозподілу регулюванням за нижнім б'єфом
| <== попередня сторінка | | | наступна сторінка ==> |
| Сутність ММП полягає в тому, що за якісну оцінку параметра а беруть таке значення аргументу, що приводить функцію L до максимуму. Рівняння (4.14) розв’язують при умові | | | Оцінка параметрів розподілу за допомогою надійних інтервалів |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |