• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Оцінювання параметрів закону розподілу

Відомо, що випадкова величина Х характеризується законом розподілу, що має деякі невідомі параметри а ( а₁, а₂, ..., а_k ) (§ 2.4).Якщо в результаті виконаного експерименту нами отримано статистичний ряд Х₁, Х₂, ... , Х_п , то очевидно можна знайти надійну оцінку параметра а.

Припустимо, що на основі обробки статистичного ряду отримано параметр , що буде оцінкою невідомого параметра а. Разом з тим, він буде функцією від випадкових величин Х₁, Х₂, ... , Х_п, тобто

= (Х₁, Х₂, ... , Х_п). (4.10)

Таким чином і обчислений параметр буде випадковою величиною, закон розподілу якого залежить від закону розподілу випадкової величини Х і від числа експериментів п. При цьому оцінка буде мати практичну цінність, якщо володіє властивостями:

1. Незміщенності. При цьому повинна виконуватися умова

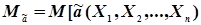= а , (4.11)

де а - істинне значення параметра.

2. Обгрунтованності. Тобто по ймовірності вона сходиться до оцінюванного параметра при нескінченному збільшенні кількості дослідів, тобто

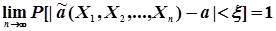, (4.12)

де x- як завгодно мале позитивне число.

Для цього потрібно, щоб дисперсія оцінки а наближалась до нуля при n®¥ , тобто

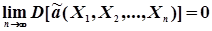
3. Ефективності. Це означає, що дисперсія оцінки а повинна бути мінімальною, тобто

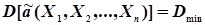. (4.13)

При цьому буде мінімальна ймовірність появи грубої помилки при визначені наближеного значення невідомого параметра.

Таким чином при розробці методів обробки статистичних даних для визначення оцінок наближених значень невідомих параметрів треба виходити із їх властивостей. Оцінки параметрів закону розподілу, що відповідають всім трьом властивостям називають доброякісними.

Практично розроблено три способи визначення оцінок: 1) метод моментів, 2) метод максимальної правдоподібності (ММП) і 3) метод найменших квадратів (МНК).

В методі моментів значення теоретичних моментів заміняють значеннями емпіричних моментів, які обчислюють за результатами статистичних рядів, чи статистичної сукупності §4.4.

В методі максимальної правдоподібності(ММП), розробленого Р.Фішером розглядають значення випадкових величин x₁ ,x₂,…,x_n, що отримані при проведенні дослідів і використовують їх для визначення невідомого параметра а. Якщо щільність розподілу j(х, а)залежить від параметра а, то в ММП задаються правдоподібною функцією, виходячи з того, що всі х_і незалежні

L(x₁ ,x₂,…,x_n, a ) = j (х₁, а) j (х₂, а)… j (х_n, а). (4.14)

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. IV. ВИСТАВКА ТА ОЦІНЮВАННЯ РОБІТ
3. IV. Загальна схема поточного і підсумкового контролю та оцінювання знань студентів
4. V. КРИТЕРІЇ ОЦІНЮВАННЯ КУРСОВОЇ РОБОТИ
5. VII розділ. Маркетингові рішення з розподілу та збуту товару
6. X. Оцінювання виробів та відбір їх на виставку.
7. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
8. Автоматизація водорозподілу з комбінованим регулюванням
9. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
10. Автоматизація водорозподілу регулювання зі сталими перепадами
11. Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
12. Автоматизація водорозподілу регулюванням за верхнім б'єфом

Переглядів: 554