• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Закони розподілу випадкової величини

Законом розподілу випадкової величини називається співвідношення, що встановлює зв'язок між можливими значеннями випадкової величини і відповідними їм ймовірностями.

Найпростішою формою завдання такого закону служить таблиця, в якій перераховані можливі значення випадкової величини і відповідні їм ймовірності.

Таблиця 1.3. Значення випадкової величини і відповідні їм ймовірності

Х1	Х2	Х3	...	Хn	Разом
Р1	P2	P3	...	Pn	=1

Щоб надати ряду розподілу наочний вигляд, будують його графічне зображення у вигляді гістограми, полігону, кумуляти і огіви.

Табличний розподіл можливих значень випадкової величини і відповідних їй ймовірностей, графічне зображення кривих розподілу і аналітичний опис вказаної залежності є форми закону розподілу.

Криві розподілу можуть бути самої різної форми. Проте серед них слід виділити так звані одновершинні криві, що часто зустрічаються.

В економічних дослідженнях симетричні розподіли зустрічаються рідко. Набагато частіше вершина кривої знаходиться не в центрі, а дещо зміщена. Зустрічається також двопіковий розподіл. Його наявність свідчить про те, що розглядається неоднорідна сукупність.

Теоретичними розподілами в економічних дослідженнях головним чином закон є Пуассона, показовий, біномінальний, Ст’юдента, 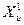- квадрат, Лапласа, нормальний та ін.

Нормальний закон розподілу реалізується для випадкових величин, які формуються під сумарною дією багатьох незалежних поміж собою дрібних причин, дія кожної з яких мала в порівнянні із загальним результатом.

У математичній статистиці нормальний розподіл відіграє роль стандарту, з яким порівнюються інші розподіли.

Формула нормальної кривої має наступний вигляд:

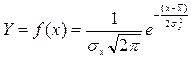, (1.15)

де Х - випадкова величина;

- середнє арифметична або математичне очікування;

σ_х - середнє квадратичне відхилення;

π =3,14159, е=2,71828 - відомі константи.

Крива Гауса - Лапласа має горбоподібний вигляд і симетрично розташовується відносно вертикальної прямої (рис. 1.1). Центр угрупування випадкової величини і форму нормальної кривої визначають числові характеристики і σ_х.

При Х= функція має максимум, рівний

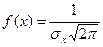. (1.16)

Симетрія кривої Х= вважається основною властивістю нормального розподілу: однакові відхилення значення випадкової величини від її середнього в обидві сторони зустрічаються однаково часто.

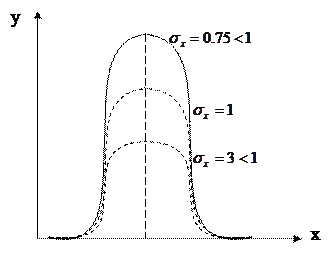Рис. 1.1. Крива Гауса - Лапласа

При збереженні своєї загальної форми крива розподілу нормального закону може мати різний ступінь пологості й крутизни залежно від значення σ_х.

У математико-статистичних дослідженнях, незалежно від розмірності випадкової величини Х, може бути визначена відносна частота.

По правому 3σ величина абсолютного відхилення випадкової величини від середнього по вибірці менше ± 3σ_х з вірогідністю 0,997. Лише 0,3% всього Хi числа спостережень виходить з "трисигмових меж". В інтервалі від Х-σ_х до Х+σ_х знаходиться 68,3% спостережень, в інтервалі від Х-2σ_х до Х+2σ_х - 95,5% спостережень. Як було сказане вище, максимум

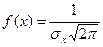. (1.17)

Оскільки площа диференційованої функції нормального розподілу дорівнює одиниці, то зі зростанням σ_х максимальна ордината нормальної кривої убуває, а сама крива стає більш пологою. Навпаки, з убуванням σ_х нормальна крива стає більш гостроверхою.

При =0 і ух=1 нормальну криву називають нормованою:

. (1.18)

Величина табульована і може бути визначена з відповідних математико-статистичних таблиць (диференціальна функція Лапласа). У цих таблицях наведені функції f(х), відповідні позитивним значеннях Х. Для від’ємних Х користуються тими ж таблицями, оскільки функція f(х) парна, тобто f(-х)=f (x). У таблиці наводяться значення f(х) для Х від 0 до 4 через 0,01.

Для того, щоб можна було користуватися готовими таблицями, потрібно криву нормального розподілу привести до стандартної форми. Стандартизація полягає в переході від випадкової величини Х, має математичне очікування і середньоквадратичне відхилення σ_х, до допоміжної величини називаної центрованим і нормованим відхиленням:

t= 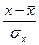чи ∆Х=t σ_х (1.19)

Використовуючи відповідні таблиці значень, будують таблицю стандартизованого розподілу вірогідності.

Якщо на вісь абсцис нанести значення t, а на вісь ординат вірогідність P(t), то графічне зображення дає нормальну криву. Фізичне значення t означає, на скільки середньоквадратичних відхилень σ_х змінюється значення випадкової величини від її середнього значення .

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. IV. Закони ідеальних газів.
3. VII розділ. Маркетингові рішення з розподілу та збуту товару
4. А) Грошовий обіг. Закони.
5. А) оптимальне значення величини зварювального струму; б) підвищене значення величини зварювального струму; в) низьке значення величини зварювального струму.
6. Абсолютні величини
7. Абсолютні і відносні величини
8. Абсолютні і відносні статистичні величини
9. Абсолютні, відносні та середні величини.
10. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
11. Автоматизація водорозподілу з комбінованим регулюванням
12. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.

Переглядів: 1197