• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Статистичні гіпотези та їх перевірка

При вибіркових обстеженнях допускаються різного роду похибки, при цьому розрізняють грубі, систематичні й випадкові помилки.

Грубі помилки за абсолютними величинами значно відрізняються від всього ряду помилок і підлягають виключенню з ряду спостережень.

Систематичні помилки є наслідком впливу певних чинників, що спотворюють результати вимірювань за певним законом у відомому напрямі. Вони викликані зносом засобів вимірювання, їх неправильною установкою, дією зовнішнього середовища і т.п.

Випадковими називають такі помилки, характер зміни яких не володіє видимою закономірністю. Кожна подальша помилка за абсолютним значенням може бути більше або менше попередньої.

Аналіз випадкових похибок ґрунтується на теорії випадкових помилок, яка дає змогу з певною гарантійною вірогідності обчислити дійсне значення шуканої величини.

В основі теорії випадкових помилок лежать наступні підтверджені досвідом висновки:

1. Різниця у значеннях характеристики вибіркової і генеральної сукупності складе помилку вибірки 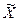– =e_х, 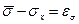і т.п. Ці помилки є випадковими величинами. Тому необхідно в кожному конкретному випадку визначити не тільки розмір помилки, але і надійність або гарантію того, що цей розмір не буде перевищений.

2. Вибіркові середні також симетрично розподіляються навкруги генеральної середньої, незалежно від характеру розподілу випадкової величини в генеральній сукупності.

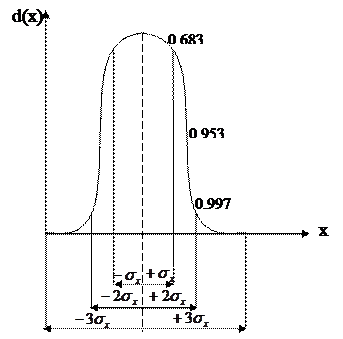Закономірність розподілу випадкових помилок спостережень описується нормальною кривою (рис. 1.2). Карл Гаус (1777-1855 рр.) використовував її як основу для теорії випадкових помилок вимірювань.

Рис. 1.2. Крива розподілу випадкових помилок спостережень

Вся площа під кривою дорівнює 1. Основна маса випадкових помилок групується навколо середнього значення, яке дорівнює 0.

На ділянці, обмеженій +σ_х, знаходиться 68,3% всіх спостережень; на ділянці, обмежений +2σ_х і –2σ_х –95,3%; на ділянці, обмеженій +3σ_х і –3σ_х –99,7%.

На основі характерних властивостей розподілу випадкових помилок спостережень можна зробити висновок, що при достатньо великому обсязі вибірки n її числові характеристики за вірогідністю наближаються до відповідних значень характеристики генеральної сукупності.

Рівень значущості звичайно вимірюється у відсотках і їх чисельне значення заснована на так званому принципі незалежності маловірогідних подій. На практиці звичайно приймають рівні значущості, що знаходяться між 0,01-0,05. Відповідно їх називають одновідсотковими, двовідсотковими і т.п.

З принципу неможливості маловірогідних подій випливає наступний висновок: якщо випадкова подія має вірогідність дуже близьку до одиниці, то практично можна вважати, що в одиничному випробуванні ця подія наступить (P³0,99).

Припущення щодо закономірностей, які мають місце в генеральній сукупності, називається статистичною гіпотезою, а критерій її перевірки - статистичною характеристикою.

Як критерій перевірки вибирається деяка статистична характеристика. Припущення, що висувається, може бути помилковим, внаслідок вибіркової помилки, і має назву нульової гіпотези Н_о.

Конкуруюча (протипожежна) гіпотеза означає, що має місце суттєва відмінність між вибірковими значеннями в генеральній сукупності. Сформулювавши гіпотезу Н_о, можна зіткнуться з чотирма ситуаціями:

- гіпотеза Н_о правильна, а її забракували, оскільки характеристика потрапила в критичну область, тобто допущена помилка першого роду, вірогідність якої рівна рівню значущості α;

- гіпотеза правильна і її прийняли, оскільки характеристика потрапила в допустиму область, тобто рішення правильне;

- гіпотеза неправильна і її прийняли, оскільки характеристика потрапила в критичну область, тобто рішення правильне;

- гіпотеза неправильна, а її відкинули, оскільки характеристика потрапила в допустиму область. Допущена помилка другого роду, тобто прийнята невірна гіпотеза.

Як видно, рівень значущості можна тлумачити як ризик вчинити помилку першого роду, тобто забракувати правильну вірну гіпотезу. В зв'язку з цим для ухвалення гіпотези рівень значущості призначають п'ятивідсотковий (α=0,05), а для бракування гіпотези - одновідсотковий (α=0,01).

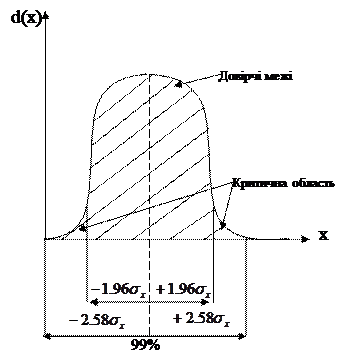
Областю ухвалення гіпотези називають сукупність значень вибраного критерію, при яких гіпотезу приймають, критичною областю - при значеннях критеріях, коли нульову гіпотезу відкидають (рис. 1.3).

Вибіркова середня є певне число, яке можна розглядати як випадкову величину. Отже можна говорити про її розподіл і про числові характеристики цього розподілу ( 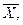σ_х², σ_х та інш.).

Двостороння область, в яку повинна потрапити середня генеральної сукупності, визначається довірчими межами при певному рівні значущості 2Ф(t)=0,95 або за інтегральною функцією Лапласа t=1,96.

Інтервал Х±1,96 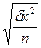означає, що з вірогідністю P=0,95 генеральна середня потрапляє в довірчі межі, а з вірогідністю P=0,05 лежить зовні цих меж, тобто потрапляє в критичну область. Міра можливої відмінності між вибірковою середньою і середньою генеральної сукупності має назву стандартної помилки.

Слід мати на увазі, що вибіркові середні, як і випадкові помилки спостережень, симетрично розподіляються навколо генеральної середньої за умови, що обсяг вибірки складає n≥30 спостережень. При малому обсязі вибіркових даних n≥30 розподіл вибіркових середніх відрізняється від нормального тим більше, чим менше обсяг вибірки.

Межі довірчого інтервалу при малих вибірках n≥30 обмежується коефіцієнтом t_α, який був запропонований в 1908 р. англійським математиком і хіміком В.С. Госсетом, який публікував свої роботи під псевдонімом "Ст’юдент" - студент. Надалі цей коефіцієнт отримав назву коефіцієнт Ст’юдента це спеціально розроблені таблиці з урахуванням обсягу вибірки).

Доцільно дотримуватися такої послідовності попередньої обробки результатів спостережень при n≥30:

1.Результати спостережень записують в таблицю.

2.Обчислюють середнє значення з n спостережень:

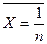
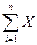_i. (1.20)

3. Визначають похибки окремих спостережень:

ΔХ_i= –X_i та їх квадрати (ΔХ_i)²_.

4. Відсіюють спостереження, різко відмінні від інших. Для цього знаходять:

4.1.Середню квадратичну похибку:

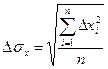. (1.21)

4.2.Задаються значенням похибки α =0,95

4.3.Визначають коефіцієнт Ст’юдента t_α=(n) для заданої надійності P і кількості спостережень n

4.4.Знаходяться межі довірчого інтервалу (похибки результатів спостережень):

ΔХ= t_α(n) Δσ_х, Х= ± ΔХ.

4.5.Обчислюють відносну похибку вибіркових даних:

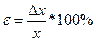. (1.22)

Читайте також:

1. II. Перевірка домашнього завдання.
2. II. Перевірка домашнього завдання.
3. II. Перевірка домашнього завдання.
4. II. Перевірка домашнього завдання.
5. II. Перевірка домашнього завдання.
6. II. Перевірка домашнього завдання.
7. II. Перевірка домашнього завдання.
8. II. Перевірка домашнього завдання.
9. II. Перевірка домашнього завдання.
10. IV. Перевірка розв’язання і відповідь
11. Абсолютні і відносні статистичні величини
12. Абсолютні статистичні показники.

Переглядів: 685