• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Метод віток і меж

Метод віток і меж використовується як до повністю цілочисельних задач, так і до частково цілочисельних задач.

Спочатку розв'язується ослаблена задача без обмежень на цілочисельність.

. (5.14)

повинна бути цілочисельною .

Тоді сфера допустимих рішень розбивається на дві підмножини і 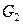таким чином, що:

:

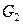: . (5.15)

Таким чином виключається інтервал , який не містить цілочисельних точок.

Початкова задача розбивається на дві підзадачі. В кожній з областей , 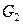знаходяться оптимальні точки, і, якщо вони не задовольняють умові цілочисельності, знову здійснюється розгалуження. Якщо отриманий оптимум виявляється допустимим (цілочисельним) для даної задачі, він фіксується і наголошується як найкращий. При цьому немає необхідності продовжувати галуження цієї підзадачі, оскільки поліпшити це рішення не вдасться.

Як тільки отримане допустиме (цілочисельне) рішення іншої підзадачі виявляється краще, воно фіксується замість попереднього.

Процес галуження продовжується до тих пір, поки кожна підзадача не призведе до цілочисельного рішення, або не буде встановлена неможливість поліпшення наявного рішення. Висновок про необхідність подальшого розбиття задачі робиться на основі введення межі.

Як межа використовується значення цільової функції отриманого допустимого цілочисельного рішення. Якщо будь-яке оптимальне рішення підзадачі забезпечує гірше значення цільової функції, ніж наявне рішення (прийняте як межа), то цю підзадачу розглядати далі не слід.

Алгоритм методу віток і меж є ітеративним.

- номер ітерації; - оцінка (для задачі мінімізації ).

При використанні алгоритму потрібне вирішення послідовності задач лінійного програмування без обмежень на цілочисельність. Послідовність задач, що підлягають вирішенню називається основним списком.

1. Якщо основний список порожній – закінчення алгоритму, інакше – вибирають задачу з основного списку і знаходять її оптимальне рішення.

2. Якщо вибрана задача не має рішення, або її оптимальне рішення гірше прийнятої оцінки, то необхідно виключити цю задачу із списку і перейти до п. 1, інакше – до п. 3.

3. Якщо отримане рішення цілочисельне – сформувати нову оцінку 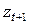, яка відповідає якнайкращому оптимальному рішенню поточної задачі. Перехід до п. 1. Якщо рішення поточної задачі нецілочисельне, то оцінка залишається у наступному вигляді: .

4. Вибирається одна із змінних , яка за умовою повинна бути цілочисельною. Проводиться розгалуження, тобто в основний список додається дві підзадачі, для яких зберігаються ті ж обмеження, але для однієї:

, (5.16)

а для іншої:

. (5.17)

Перехід до п. 1.

Слід відзначити, що вибір змінної може бути довільним (за збільшенням номерів) або визначатися таким чином:

1) представлена змінна є важливим рішенням, що приймається в рамках розробленої моделі;

2) коефіцієнт в цільовій функції істотно перевершує всі інші.

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. D) методу мозкового штурму.
3. Demo 11: Access Methods (методи доступу)
4. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
5. I Метод Шеннона-Фано
6. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
7. I. Метод єдиної подібності.
8. I. Метод рiвних вiдрiзкiв.
9. II. МЕТОДИЧНІ ВКАЗІВКИ
10. II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
11. IV. КЕРІВНИЦТВО, КОНТРОЛЬ І НАДАННЯ ОРГАНІЗАЦІЙНО-МЕТОДИЧНОЇ ДОПОМОГИ ПРАКТИКАНТАМ.
12. IV. Метод супутних змін.

Переглядів: 698