
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Моделювання процесу обслуговування в СМО.
Функція розподілу проміжку між викликами  , а функція розподілу тривалості обслуговування
, а функція розподілу тривалості обслуговування  . Програма моделювання має містити два генератора випадкових величин z и x із заданими функціями A(t) и B(t), змінні to збереження моменту надходження чергового виклику та t1, t2,..., tv для збереження моменту звільнення i-го (
. Програма моделювання має містити два генератора випадкових величин z и x із заданими функціями A(t) и B(t), змінні to збереження моменту надходження чергового виклику та t1, t2,..., tv для збереження моменту звільнення i-го (  ) каналу.
) каналу.
Для спрощення пояснень приймемо v = 3 и проаналізуємо роботу алгоритму з моменту надходження п’ятого виклику. Перший генератор формує чергове випадкове число z5, що відповідає надходженню п’ятого виклику  . Припустимо, що до моменту
. Припустимо, що до моменту  перший канал був зайнятий четвертим викликом, а другий і третій, відповідно другим і третім. Тоді:
перший канал був зайнятий четвертим викликом, а другий і третій, відповідно другим і третім. Тоді:  ,
,  ,
,  . Кожне з чисел t1 , t2,, t3 визначає момент звільнення відповідного каналу.
. Кожне з чисел t1 , t2,, t3 визначає момент звільнення відповідного каналу.
При послідовному занятті каналів значення to почергово порівнюється з t1, t2,, tv, поки не знаходиться комірка з моментом звільнення 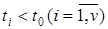 . Припустимо, що
. Припустимо, що 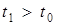 и
и 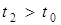 , а
, а 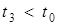 . Це означає, що до моменту надходження п’ятого виклику перший і другий канал були зайняті, а третій вже звільнився і може прийняти на обслуговування п’ятий виклик. Тоді t3 присвоюється t0, потім генерується випадкове число x5, що визначає тривалість обслуговування п’ятого виклику. Доданням числа x5 до t3 п’ятий цикл закінчується.
. Це означає, що до моменту надходження п’ятого виклику перший і другий канал були зайняті, а третій вже звільнився і може прийняти на обслуговування п’ятий виклик. Тоді t3 присвоюється t0, потім генерується випадкове число x5, що визначає тривалість обслуговування п’ятого виклику. Доданням числа x5 до t3 п’ятий цикл закінчується.
Шостий цикл починається з генерації випадкового числа z6. Як раніше, t0=t0+z6. Потім здійснюється почергове порівняння вмісту нульової комірки з вмістом решти комірок. Якщо тепер виявиться, що 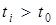 ,
, 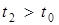 і
і  , то шостий виклик буде втрачений і на цьому цикл закінчиться.
, то шостий виклик буде втрачений і на цьому цикл закінчиться.
Для підрахунку числа надійшедших Квик і втрачених Квт. викликів використовують два лічильники. В перший додається одиниця при кожній генерації числа z, а в другий - при кожній втраті виклику. Відношення Квик/Квт. дає по закінченні чергової серії статистичну оцінку втрат викликів.
2. Порядок виконання роботи:
2.1. Початкові умови моделювання:
a) Параметр потоку: 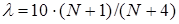 (викл./хв), де N - номер за журналом.
(викл./хв), де N - номер за журналом.
b) Середній час обслуговування h і число каналів v:
| N | |||||||||||||||||||||||||
| v | |||||||||||||||||||||||||
| h,с |
c) На початку моделювання в системі зайнято два канали.
2.2. Порядок моделювання.
a) Моделювання здійснювати на інтервалі: [t1, t2]хв.
t1=N+1, t2=N+200,де N - номер за журналом.
b) Надходження виклику моделюється аналогічно лабораторній роботі №1, запам’ятовується в змінній tнад і підраховується лічильником Квик.
c) Процес обслуговування моделюється за експоненціальним законом розподілу.
 ;
; 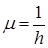 .
.
d) Час звільнення каналу визначається: tзв.i = tнад.i + xi;
e) Канали займаються послідовно. Якщо до моменту надходження виклику зайняті всі канали, то він втрачається і підраховується кількість втрачених викликів Квт.
Результати моделювання зводяться в таблицю:
| r | z | 
| tнад | tзв | N каналу |
| r1 | - | x1 | - | t0 + x1 | |
| r2 | - | x2 | - | t0 + x2 | |
| r3 | z3 | x3 | tнад.3 | tнад.3 + x3 | Втрата |
2.3. Визначити модельну імовірність втрати виклику:

Квт - кількість втрачених викликів;
Квик - загальна кількість викликів
2.4. Визначити Рв за I формулою Ерланга: 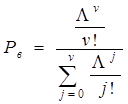 ,
,
де  .
.
Зробити висновки.
3. Контрольні питання.
3.1. Визначення та практичне вимірювання характеристик якості систем з втратами:
- імовірність втрати виклику;
- імовірність втрати за часом;
- імовірність втрати за навантаженням.
3.2. Використання символіки Кендала-Башаріна.
3.3. Побудувати граф станів системи, що моделювалась. Визначити типи потоків.
ЛАБОРАТОРНА РоБОТА №5
Аналіз V-канальної СМО з явними втратами
Мета: Дослідити 1-й розподіл Ерланга і характеристики якості СМО з явними втратами.
Читайте також:
- D моделювання ландшафтних комплексів
- D – моделювання в графічній системі КОМПАС
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- II. Вантажне господарство. Пристрої для обслуговування пасажирів
- II. Поняття соціального процесу.
- IV. План навчального процесу.
- А. Особливості диференціації навчального процесу в школах США
- А. Особливості диференціації навчального процесу в школах США
- Автоматизація процесу абсорбції
- Автоматизація процесу адсорбції
- Автоматизація процесу випарювання
- Автоматизація процесу відстоювання
| <== попередня сторінка | | | наступна сторінка ==> |
| Основні характеристики якості системи M/M/v/L | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |