Визначення

Дедуктивним висновком називається висновок формули В з формули А, заснований на тому, що В є логічним наслідком А.

Приклад.Довести правильність міркування за дедукцією: «Резолюція ухвалюється, якщо і тільки якщо за неї голосує більшість депутатів. За резолюцію не проголосувала більшість депутатів, тому резолюція не ухвалюється».

Розв'язок. Засновками у цьому висновку є висловлення «Резолюція приймається, якщо і тільки якщо за неї голосує більшість депутатів» і «За резолюцію не проголосувала більшість депутатів», а висновком — «Резолюція не приймається». Введемо такі атоми:

Р — «за резолюцію проголосувала більшість депутатів»;

Q — «резолюція приймається».

Тоді засновки і висновок позначимо відповідно через Р ~ Q, Ø Р, ØQ, приєднаємо за допомогою імплікації до кон'юнкції засновків (Р ~ Q)л (ØР)висновок (ØQ) і перевіримо, наприклад, за допомогою тотожних перетворень, чи є імплікація ((Р ~ Q) Ù Ù(ØР)) ®(ØQ) логічним законом.

((Р ~ Q) Ù (ØP)) ® (ØQ)= (ØР Ú Q)Ù(Р Ú ØQ)Ù (ØР)) ® (ØQ) = — виразили еквівалентність через кон'юнкцію, диз'юнкцію та заперечення (див. (5.1)).

((ØР Ú Q) Ù (ØР) Ù (Р Ú ØQ)) ® (ØQ) = — застосували комутативний закон.

((ØР) Ù (Р Ú ØQ)) ® (ØQ) = — використовували закон поглинання.

((ØР Ù Р) Ú (ØР Ù ØQ)) ® (ØQ) = — застосували дистрибутивний закон.

(ØР Ù ØQ) ® (ØQ) = — використовували закон суперечності.

Ø(ØР Ù ØQ) Ú (ØQ) = — виразили імплікацію через заперечення та диз'юнкцію. Тепер розкриємо дужки і застосуємо закон виключеного третього:

Р Ú Q Ú ØQ = І.

Одержано істинне висловлення. Отже, висновок виходить з засновків, і задане міркування задовольняє визначення дедуктивного висновку. Істинність висновку в дедуктивному висновку гарантується істинністю засновків.

Твердження 1.Висловлення В є логічним наслідком висловлення А,якщо висловлення А ® ØВ є тотожно хибним.

Твердження 2.Висловлення В є логічним наслідком висловлення А, якщо на всіх інтерпретаціях, на яких А істинне, В теж істинне.

Тотожна істинність або хибність засновку імплікації дозволяє зробити висновок про істинність або хибність наслідку.

Твердження 3. Якщо висловлення В є логічним наслідком висловлення А і висловлення А — тотожно істинне висловлення, висловлення В також є тотожно істинним.

Твердження 4. Якщо висловлення А є тотожно хибним, то для будь-якого висловлення В правильно, що А ® В.

При створенні математичної логіки переслідувалася ціль побудови формальної мови для математичних міркувань і доведень. У математиці і «чистій» логіці доводять теореми, тобто виводять наслідки з певних припущень. Припущення називаються аксіомамиабо гіпотезами, при цьому передбачається, що вони тотожно істинні у всій розглянутій теорії. Доведенняявляє собою логічний висновок списку висловлень. Додавання висловлення у список доведення можливе, якщо дане висловлення є наслідком висловлень, внесених до цього списку раніше, або якщо воно є аксіомою чи гіпотезою. Теорема вважається доведеною, якщо твердження теореми записане у список доведення, тобто якщо встановлено, що твердження теореми є логічним наслідком введених аксіом.

Правила для дедуктивного висновку будуються на підставі загальнозначущих формул логіки висловлень виду А ® В. Ці правила часто записують як правила формального висновку у такому вигляді:

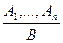
Тут А₁,..., А_n — засновки висновку, а В — наслідок. Тавтологія, що відповідає такому правилу, — А₁ Ù А₂Ù ... Ù А_п®В. Найбільш часто використовувані правила дедуктивного висновку наведено у таблиці 5.5.

Таблиця 5.5. Правила дедуктивних висновків логіки висловлень

Правило дедуктивного висновку	Тавтологія	Назва правила

	А ® (A Ú В)	Правило введення диз'юнкції
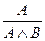
A,	((А) Ù (В)) ® (А Ù В)	Правило введення кон'юнкції
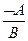
A Ú В	(A Ú В) Ù ØА ® В	Правило видалення диз'юнкції (Диз'юнктивний силогізм)
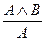
	(А Ù В)®А	Правило видалення кон'юнкції
	(А ® B) ® (ØВ®ØА)	Правило контрапозиції імплікації
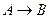
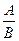
	(А Ù (А® В))® В	Правило відділення (Modus Ponens)
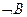
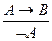
	(ØВ Ù (А®В))®ØА	Від'ємна форма правила відділення (Modus Tollens)
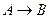
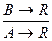
	((А ® В) Ù (В ® R))® ®(А ®R)	Гіпотетичний силогізм

З усіх правил, наведених у таблиці 5.5, найбільш часто використовується правило відділення. Правило відділення має такий логічний сенс: якщо засновок правильний, то правильний і наслідок з нього. Наведемо приклади міркувань за допомогою правила відділення:

«Якщо студент не вивчив теорію, то він не виконає завдання. Студент не вивчив теорію. Отже, студент не виконає завдання».

«Якщо студент одержав п'ять, значить, він розв'язав задачу. Студент одержав п'ять. Отже, студент розв'язав задачу».

Приклад.Дано істинне висловлення «Якщо п ділиться на 9, то п ділиться на 3». Нехай також відомо, що «n ділиться на 9». Який висновок можна зробити, виходячи з цих двох висловлень?

Розв'язок. Введемо атомарні висловлення:

А — « п ділиться на 9 »;

В— «п ділиться на 3».

Висловлення «Якщо п ділиться на 9, то п ділиться на З» можна зобразити у вигляді формули А ® В. З одночасного виконання засновків А ® В і А можемо зробити висновок В за правилом відділення: «п ділиться на 3».

Приклад.Визначте тип Правила дедуктивного висновку, яке було використане у такому міркуванні: «Температура повітря +1 °С, і йде дощ. Отже температура повітря +1°С».

Розв'язок. Введемо атоми:

А— «Температура повітря +1°С»;

В — «Йде дощ».

Висловлення «Температура повітря +1 °С, і йде дощ» можна зобразити у вигляді формули А Ù В,аодержаний висновок «температура повітря +1°С» є висловлення А. Очевидно, що висновок зроблено відповідно до правила видалення кон'юнкції (див. табл. 5.5).

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Визначення	\|	Теорема 1

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.01 сек.