
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Визначення
Визначення
Дійсне число Т(р) з інтервалу [0, 1], яке ставиться у відповідність висловленню р, називають значенням істинності висловлення р.
Значення істинності Т(р) можна розуміти як ймовірність того, що висловлення р істинне, причому два висловлення, що мають одне й те ж значення істинності, можна вважати логічно еквівалентними. Значення істинності Т(р) = 1 означає істинність, а значення Т(р) = 0 — хибність висловлення р. Заперечення Øр визначається за допомогою значення істинності таким чином: Т(Øр) = 1 - Т(р).В трьохзначній логіці, наприклад, як значення істинності можна прийняти числа 0, 1/2 і 1. Якщо значення істинності Т(р) = 1/2, то значення істинності Øр також дорівнює 1/2, і р виявляється логічно еквівалентним своєму запереченню. Таке висловлення може бути назване сумнівним, причому заперечення цього висловлення також виявляється сумнівним. Зазначений підхід свідчить про наявність тісного зв'язку між багатозначними логіками і теорією ймовірностей.
Багатозначна логіка розглядає однорідні логічні функції, що визначені на множині (0, 1, ..., k - 1), яка складається з k елементів. В силу однорідності сама функція k-значної логіки від п змінних приймає значення з тієї ж скінченної множини.
Функції k-значної логіки визначені і приймають значення, що входять до деякої множини Вk = {0, 1, ..., k - 1}, що називається алфавітом цієї логіки.
Функцію k-значної логіки однозначно визначає її таблиця значень (істинності). Множину всіх функцій k-значної логіки позначають Pk. Кількість функцій Pk, що залежать від п змінних, дорівнює 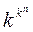 . Як і у двозначній логіці, висловлення зображуються у вигляді формул k-значної логіки. Елементарні функції зображують узагальнення аналогічних функцій двозначної логіки. Розглянемо основні функції k‑значної логіки.
. Як і у двозначній логіці, висловлення зображуються у вигляді формул k-значної логіки. Елементарні функції зображують узагальнення аналогічних функцій двозначної логіки. Розглянемо основні функції k‑значної логіки.
Унарні функції
1. Циклічне заперечення:
Øх = х + l(mod k),
де у mod k — залишок від ділення у на k.
Таким чином, ця елементарна функція зображує узагальнення заперечення у розумінні «циклічного» зміщення значень:

2.Заперечення Лукашевича:
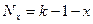 .
.
Наведена елементарна функція Nx є іншим узагальненням операції заперечення у розумінні «дзеркального» відображення значень.
3. Узагальнене заперечення:

Елементарна функція Іσ(х)при σ ¹ k – 1 є узагальненням деякихвластивостей заперечення.
4. Характеристична функція:
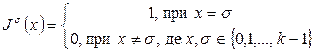
Функція Jσ(x) — характеристична функція значення а приσ ¹ k – 1 зображує узагальнення операції заперечення.
Бінарні функції
1. Узагальнення кон'юнкції:
min(xi, хj).
2. Інше узагальнення кон'юнкції:
xi хj (mod k).
3. Узагальнення диз'юнкції:
max(xi, хj).
Визначення
Система функцій f1... fn називається повною, якщо будь-яка функція з Pk може бути зображена у вигляді формули, що складається з цих функцій.
В k-значній логіці залишаються справедливими деякі закони двозначної, а саме: асоціативності, комутативності, дистрибутивності і т. д. Подібно до функцій двозначної логіки k-значні логічні функції можуть бути задані у вигляді таблиці. Кількість стовпців у таблиці дорівнює kn, де п — кількість змінних, що входять до функції, а кількість функцій визначається числом  ,яке швидко зростає із збільшенням k.
,яке швидко зростає із збільшенням k.
В k-значній логіці існує k констант f0 =0, f1 = 1, ..., fk-1 = k - 1. Серед функцій однієї змінної найбільш часто використовуваними є такі:
1) Характеристичні функції i-го порядку — f0(x), f1(x), f2(x),що визначені в таблиці 5.17.
Таблиця 5.17. Функції однієї змінної у трьохзначній логіці
| X | ||||
| F(x) | x | |||
| f0(x) | ||||
| f1(x) | ||||
| f2(x) | ||||
| Nx | ||||
| Øx |
2) Заперечення Лукашевича Nx = k - 1 - х.
3) Функція циклічного заперечення Øх = х + 1 (mod). Таблиці істинності вказаних функцій у трьохзначній логіці будуть мати вигляд, що зображений у таблиці 5.17. Серед функцій двох змінних найбільш важливе значення мають такі:
1) значна диз'юнкція — x1 Ú х2= mах(x1, х2).
2) значна кон'юнкція — х1Ù х2 = mіn(х1, х2).
3) Функція Шеффера — Веббах — х1|х2 = x1 Ú х2 + l(mod k).
4) Додавання за модулем k – x1+ x2 (mod k).
5) Множення за модулем k – х1* х2 (mod k).
Значення даних функцій при k = 4 зображено в таблиці 5.18.
Таблиця 5.18. Функції двох змінних у чотиризначній логіці
| x1 | ||||||||||||||||
| x2 | ||||||||||||||||
| x1 Ú х2 | ||||||||||||||||
| х1Ù х2 | ||||||||||||||||
| x1 Ú х2+ l(mod k) | ||||||||||||||||
| x1 + х2(mod k) | ||||||||||||||||
| х1* х2 (mod k) |
Скориставшись поняттям характеристичних функцій для двозначного випадку, нескладно записати ДДНФ і ДКНФ у багатозначній логіці. Нагадаємо, що основну роль у ДДНФ відіграють елементарні кон'юнкції 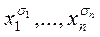 , які відмінні від нуля лише на одному наборі
, які відмінні від нуля лише на одному наборі 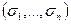 . При цьому всі вони одержані з кон'юнкції, що відповідає одиничному набору, підстановкою функції від однієї змінної xσ.
. При цьому всі вони одержані з кон'юнкції, що відповідає одиничному набору, підстановкою функції від однієї змінної xσ.
Читайте також:
- I визначення впливу окремих факторів
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- Ocнoвнi визначення здоров'я
- Алгебраїчний спосіб визначення точки беззбитковості
- Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
- Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
- Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
- Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
- Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
- Біостратиграфічні методи визначення віку порід
- Біуретовий метод визначення білків
| <== попередня сторінка | | | наступна сторінка ==> |
| Завдання | | | Системне програмне забезпечення |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |