
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Завдання
Запитання
1. Сформулюйте призначення обчислення предикатів.
2. Запишіть формули аксіом обчислення предикатів.
3. Поясніть обмеження аксіом обчислення предикатів.
4. Назвіть правила висновку обчислення предикатів.
5. Побудуйте схему правила узагальнення.
6. Визначте правило $-введення за допомогою схеми.
7. Які обмеження необхідні для правила узагальнення і $-введення? До яких наслідків може призвести недотримання вказаних обмежень?
8. Яку особливість здобуває правило підстановки в обчисленні предикатів?
9. Сформулюйте правило перейменування вільних змінних.
10.В чому полягає сутність правила перейменування зв'язаних змінних?
11.Сформулюйте твердження теореми про загально значимості правил висновку обчислення предикатів.
1. Доведіть нелогічність таких міркувань:
1.1.Всі студенти нашої групи — члени клуба «Динамо». А деякі члени клуба «Динамо» займаються спортом. Отже, деякі студенти нашої групи займаються спортом.
1.2.Деякі студенти нашої групи — вболівальники «Динамо». А деякі вболівальники «Динамо» займаються спортом. Отже, деякі студенти нашої групи займаються спортом.
1.3.Кожний першокурсник знайомий кимось з студентів другого курсу. А деякі другокурсники — спортсмени. Отже, кожний першокурсник знайомий з кимось із спортсменів.
2. Показати, що формула G не є логічним наслідком множини формул К:
а)  ,
, 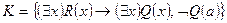 ;
;
б)  ,
, 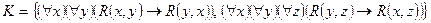 ;
;
в) 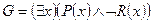 ,
,
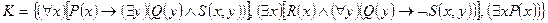
5.11. Багатозначна логіка
Виникнення багатозначних логік, значення істинності висловлення, алфавіт багатозначної логіки, унарні і бінарні функції, повна система функцій багатозначної логіки
Вперше багатозначна логіка з'явилася через заперечення аристотелева закону виключеного третього. Відповідно до цього закону диз'юнктивне висловлення р Ú Ø р є тавтологія, а атомарне висловлення р у аристотелевій логіці завжди або істинне, або хибне. Оскільки в аристотелевій логіці будь-яке висловлення може приймати тільки одне з двох значень істинності (істину або хибність), вона одержала назву двозначної логіки. В 1921 році Я. Лукашевич у маленькій статті на двох сторінках розглядає трьохзначну логіку, тобто таку логіку, в якій будь-яке висловлення р може приймати одне з трьох можливих значень істинності. Незалежно від Лукашевича Е. Пост аналізує m-значнулогіку, в якій висловлення р може приймати одне з m можливих значень істинності, де m — будь-яке ціле число, більше за 1. У випадку, коли m більше за 2, логіку називають багатозначною. В 1930 році Лукашевич і Тарський приступають до подальшого вивчення m-значної логіки. В 1932 році поняття m-значноїлогіки узагальнюється Г. Рейхенбахом, що розглядає нескінченнозначну логіку, в якій для висловлення р існує нескінченна множина значень істинності.
Видатний вчений А. Гейтінг приблизно у то й же час побудував двозначну символічну логіку, виходячи з потреб інтуїціониської математичної школи. Ця логіка, на відміну від аристотелевої, не приймає беззаперечно законів виключеного третього і подвійного заперечення. Внаслідок цього закони створеної зі спеціальними цілями логіки Гейтінга, як і закони багатозначних логік, відрізняються від законів Аристотеля. Тому такі логіки називають неаристотелевими. Символічна двозначна логіка, побудована Гейтінгом у роботі «Принципи математики», належить до неаристотелевих логік, відрізняючись від аристотелевої іншою інтерпретацією імплікації.
Подібно неевклідовим геометріям неаристотелеві логіки також знайшли собі застосування. Нескінченнозначна логіка була задумана Г. Рейхенбахом як фундамент математичної теорії ймовірності. А у 1933 році Т. Швицький помітив, що багатозначні логіки можуть бути використовувані у сучасній квантовій фізиці. Багато аспектів такого використання були досліджені Г. Біркгофом і Г. Рейхенбахом. Використання інтуїціоністами логіки Гейтінга також свідчить про математичні цінності нових логік.
Для спрощення розгляду основних положень теорії багатозначних логік обмежимося трьохзначною логікою і скористаємося методом таблиць істинності. В першу чергу, відтворимо таблицю істинності для операції кон'юнкції (таблиця 5.11).
Таблиця 5.11. Таблиця істинності кон'юнкції
| Ù | q | ||
| І | X | ||
| р | І | І | X |
| X | X | X |
Таблиця 5.11 побудована таким чином: у лівому стовпці знаходяться можливі значення істинності для висловлення р, а у верхньому рядку — можливі значення істинності для висловлення q. Знаючи значення істинності вказаних висловлень, можна знайти значення їх кон'юнкції у комірці, що стоїть на перетині рядку, що відповідає значенню істинності р, і стовпця, відповідного значенню істинності q. Оскільки, за визначенням, кон'юнкція істинна в тому і тільки в тому випадку, коли обидва висловлення р і q істинні, значення І стоїть у лівій верхній комірці таблиці, а врешті — X. Зазначимо, що таблиця заповнюється на підставі одного лише визначення операції кон'юнкції.
Тепер перейдемо до трьохзначної логіки і позначимо три можливі значення істинності висловлення через І, «?» і X. Знов складемо таблицю істинності операції кон'юнкції (таблиця 5.12). Оскільки кон'юнкція істинна, коли обидва висловлення р і q істинні, ліва верхня комірка таблиці повинна містити значення І, крім того, І не може знаходитися ні в якій іншій комірці таблиці. Таким чином, залишається вісім комірок, в кожній з яких може бути записано або значення X, або значення «?». Всього одержується 28 = 256 способів заповнення таблиці. Звідси маємо, що у трьохзначній логіці існує 256 різних визначень кон'юнкції.
Таблиця 5.12. Шаблон таблиці істинності кон'юнкції у трьохзначній логіці
| Ù | q | |||
| І | ? | X | ||
| р | І | І | ||
| ? | ||||
| X |
В таблицях 5.13 і 5.14 наведено дві з 256 можливих таблиць істинності, операції кон'юнкції у трьохзначній логіці.
Таблиця 5.13. Таблиця істинності кон'юнкції у трьохзначній логіці (Лукашевич та ін.)
| Ù | q | |||
| І | ? | X | ||
| р | І | І | ? | X |
| ? | ? | ? | X | |
| X | X | X | X |
Таблиця 5.14. Таблиця істинності кон'юнкцїі у трьохзначній логіці (Бочар)
| Ù | q | |||
| І | ? | X | ||
| р | І | І | ? | X |
| ? | ? | ? | ? | |
| X | X | ? | X |
Таблиця істинності 5.13 була запропонована Лукашевичем, Постом і Россером. Вона будується відповідно до угоди, за якою значення «?» більш хибне, ніж І, але менш хибне, ніж X, а значення кон'юнкції співпадає із значенням істинності більш хибного із складових висловлень.
Відмінне від описаного визначення кон'юнкції дає Бочар (таблиця 5.14). За Бочаром символ «?» означає нерозв'язність, а кон'юнкція висловлень р і q вважається нерозв'язною у випадку нерозв'язності хоча б одного із складових висловлень.
Розглянемо таблицю істинності операції заперечення. У випадку заперечення єдине обмеження полягає у тому, що Øр не може бути істинним при істинності висловлення р,і Øр не може бути хибним у випадку хибності р. Вказане обмеження повністю визначає таблицю істинності для заперечення у двозначній логіці і припускає 12 можливих способів визначення заперечення у трьохзначній. Нижче наведено дві з 12 можливих для заперечення таблиць істинності операції заперечення. Таблиця істинності 5.15, що запропонована Постом, заснована на угоді, згідно з якою операції заперечення привласнюється наступне за порядком значення аргументу. Таблиця істинності 5.16 була запропонована Бочаром, Лукашевичем і Россером, які виходили з того, що Ø(Øр) повинне бути еквівалентне р.
Таблиці істинності інших логічних операцій можуть бути побудовані на підставі їх визначення за допомогою операцій кон'юнкції та заперечення. Оскільки кон'юнкція та заперечення незалежні, а решта операцій може бути через них виражена, то існує взагалі 256 ´ 12 = 3072 різних трьохзначних логік. Таким чином, кількість різних можливих структур багатозначної логіки надзвичайно велика.
Таблиця 5.15. Таблиця істинності заперечення у трьохзначній логіці (Пост)
| р | Øр |
| І | ? |
| ? | X |
| X | І |
Таблиця 5.16. Таблиця істинності заперечення у трьохзначній логіці (Бочар та ін.)
| р | Øр |
| І | X |
| ? | ? |
| X | І |
В деяких випадках при побудові багатозначних логік використовується таке поняття значення істинності.
Читайте також:
- V. Завдання.
- VІ. Підсумки уроку і повідомлення домашнього завдання.
- Адаптація персоналу: цілі та завдання. Введення у посаду
- Адвокатура в Україні: основні завдання і функції
- АКТУАЛЬНI ПРОБЛЕМИ І ЗАВДАННЯ КУРСУ РОЗМIЩЕННЯ ПРОДУКТИВНИХ СИЛ УКРАЇНИ
- Актуальність і завдання курсу безпека життєдіяльності. 1.1. Проблема безпеки людини в сучасних умовах.
- Аналіз руху грошових коштів у контексті нової фінансової звітності Важливим завданням аналізу фінансового стану підприємства є оцінка руху грошових коштів підприємства.
- Аудит, його мета та завдання
- Багатокритеріальні завдання оптимального керування
- Багатокритерійні завдання і можливі шляхи їхнього рішення.
- Безпека життєдіяльності людини – найважливіше завдання людської цивілізації
- Бухгалтерська звітність, її значення, завдання і вимоги
| <== попередня сторінка | | | наступна сторінка ==> |
| Завдання | | | Визначення |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |