• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Завдання

Запитання

1. Дайте визначення випередженої нормальної форми.

2. За допомогою яких законів можна опустити знаки операцій заперечення безпосередньо на предикати?

3. Сформулюйте алгоритм перетворення виразів довільної форми у ВНФ.

4. Назвіть правила висновку, які можна використовувати для проведення дедуктивних умовиводів з висловленнями логіки предикатів.

5. В чому полягає правило видалення квантора загальності?

6. Як і навіщо використовується правило введення квантора загальності?

7. Поясніть відмінність у трактуванні елемента предметної області у правилі видалення квантора існування від прийнятої у правилі введення квантора загальності.

8. Яке правило введення квантора існування?

1. Звести до ВНФ такі вирази:

а) ;

б) ;

в) ;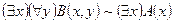

г) ;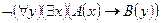

д) .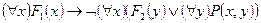

2. Визначте, чи є формула ($х) (Р(х) Ù Q(x)) логічним наслідком формул ($х) Р(х)і ($х) Q(x).

3. Застосовуючи дедуктивні правила логіки предикатів, наведіть висновки з таких засновків:

3.1.Якщо хтось з тих людей — автор цих пліток, то він глупий і безпринципний. Але ніхто з тих людей не глупий і не позбавлений принципів.

3.2.Якщо всі ці люди не хоробрі або на них не можна покластися, то вони не належать до нашої компанії. Але вони належать до нашої компанії.

3.3.Якщо хтось з підозрілих здійснив всі ці нерозкриті крадіжки, то він був ретельно підготовлений і мав співучасника. Якщо б всі крадіжки були підготовлені ретельно, то, якщо б був співучасник, вкрадено було б набагато більше. Але останнє не має місця.

3.4.Якщо один з нас піде завтра на перше заняття, то він повинен буде підвестися рано, а якщо ми підемо сьогодні ввечері у кіно, то він ляже пізно спати. Якщо будь-який з нас ляже пізно спати, а підведеться рано, то буде задовольнятися п'ятьма годинами сну. Але ми не можемо задовольнятися п'ятьма годинами сну.

3.5.В бюджеті виникне дефіцит, якщо і тільки якщо не підвищать деякі мита. Державні витрати на всі соціальні нестатки скоротяться, якщо і тільки якщо у бюджеті буде дефіцит. Деякі мита підвищать.

3.6.Якщо всі ціни одночасно підвищуються, то підвищується і заробітна плата. Всі ціни високі або застосовується регулювання цін. Якщо застосовується регулювання цін, то немає інфляції. Спостерігається інфляція.

5.10. Обчислення предикатів

Структура обчислення предикатів, правила відділення та узагальнення, правила " і $-введення, перейменування вільних і зв'язаних змінних

Аналогічно обчисленню висловлень в логіці предикатів існує формальна система — обчислення предикатів, яка займається конструюванням формул і доведенням їх загальнозначущості. Обчислення предикатів має ідентичну обчисленню висловлень структуру, а саме: мову, систему аксіом і правила висновку.

Аксіоми обчислення предикатів можна поділити на дві групи:

1) Аксіоми обчислення висловлень (можна обрати будь-яку з формальних систем S₁, S₂).

2) Предикатні аксіоми, де змінна х у формулі F(x) є вільною і жодного разу не піддається дії квантора за у:

P1) ;

P2) .

Формула F(н) одержана з F(x) заміною х на у.

Для з'ясування сенсу вимоги до входжень х у F(x)розглянемо як F(x) формулу $у Р(у, х), в якій вільне входження х знаходиться в області дії квантора $у, тобто зазначена вимога не задовольняється. Підстановка даної формули до аксіоми Р1 дає таку формулу: .

Якщо одержану формулу проінтерпретувати на множині натуральних чисел N з предикатом Р «бути більше», то одержимо висловлення: «якщо для всякого х знайдеться у, який більше нього, то знайдеться і у, більший за самого себе». Зановок цієї імплікації істинний на N, а його висновок хибний, тому всі висловлення є хибними.

В обчисленні предикатів використовуються такі правила висновку:

1) Правило відділення (Modus Ponens), сформульоване у п. 5.3 (див. таблицю 5.5), повністю переноситься з обчислення висловлень.

2) Правило узагальнення ("-введення):

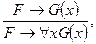
де G(x) містить вільні входження х, a F їх не містить.

3)Правило $-введення:

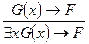
при тих же вимогах до F і G, що й у попередньому правилі.

Правило перейменування вільних змінних

В обчисленні предикатів з вивідності формули F(x), що містить вільні входження х, жодне з яких не знаходиться в області дії квантора за у, виходить вивідність F(y).

Приклад.Довести справедливість правила перейменування вільних змінних.

Розв'язок.

1. F(x) (за умови).

2. F(x)® (G ® F(x)) (аксіома 1 формальної системи S₂; тут як G можна обрати будь-яку довідну формулу, що не містить вільних входжень змінних х;довідність цієї формули знадобиться на кроці 5, а обмеження на х — на кроці 4).

3. G ® F(x) (за правилом відділення, кроки 1, 2).

4. G ® "x F(x) (за правилом узагальнення, крок 3).

5. "x F(x) (наслідок з кроку 4, оскільки G — істинна формула).

6. F(y)(крок 5, аксіома Р1)

Правило доведено.

Правило перейменування зв'язаних змінних

В обчисленні предикатів з вивідності "x F(x)виходить вивідність " у F(y),а з вивідності $х F(x)— вивідність $у F(y) за умови, що F(x) не містить вільних входжень у і містить вільні входження х, жодне з яких не входить до області дії квантора за у.

Приклад.Довести правило перейменування зв'язаних змінних для квантора загальності.

Розв'язок.

1. "x F(x) (за умови).

2. "x F(x) ® F(y) (аксіома P1).

3. "x F(x) ® "y F(y) (правило узагальнення, крок 2).

4. "y F(y) (кроки 1, З).

Необхідно зауважити, що доведення для квантора $ здійснюється аналогічно, але використовує аксіому Р2 і правило $-введення.

Теорема 1

Будь-яка довідна формула обчислення предикатів тотожно істинна.

Ця теорема аналогічна відповідній теоремі обчислення висловлень і показує, що правила висновку в обчисленні предикатів зберігають загальнозначущість, тобто їх застосування до загальнозначущих формул знов дає загальнозначущі формули.

Читайте також:

1. V. Завдання.
2. VІ. Підсумки уроку і повідомлення домашнього завдання.
3. Адаптація персоналу: цілі та завдання. Введення у посаду
4. Адвокатура в Україні: основні завдання і функції
5. АКТУАЛЬНI ПРОБЛЕМИ І ЗАВДАННЯ КУРСУ РОЗМIЩЕННЯ ПРОДУКТИВНИХ СИЛ УКРАЇНИ
6. Актуальність і завдання курсу безпека життєдіяльності. 1.1. Проблема безпеки людини в сучасних умовах.
7. Аналіз руху грошових коштів у контексті нової фінансової звітності Важливим завданням аналізу фінансового стану підприємства є оцінка руху грошових коштів підприємства.
8. Аудит, його мета та завдання
9. Багатокритеріальні завдання оптимального керування
10. Багатокритерійні завдання і можливі шляхи їхнього рішення.
11. Безпека життєдіяльності людини – найважливіше завдання людської цивілізації
12. Бухгалтерська звітність, її значення, завдання і вимоги

Переглядів: 656