• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення

Завдання

Запитання

1. Що розуміють під колізією змінних?

2. До яких наслідків може призвести перенесення квантора на початок формули? Наведіть приклади коректного і некоректного перенесення кванторів на початок формули.

3. Поясніть суть заміни зв'язаної змінної.

4. Сформулюйте комутативні властивості кванторів.

5. За дотримання якої умови правомірно використовування дистрибутивних властивостей кванторів?

6. Яким чином можна обійти обмеження дистрибутивних властивостей кванторів?

7. Запишіть формули закону де Моргана для кванторів.

1. Опустіть знаки заперечення безпосередньо на предикати або булеві змінні:

а) Ø($х) (Ø("y) (B(y)Ú ($z)С(z)) ÙØА(х)));

б) Ø("y) (Ø$х) (А(у, z)Ú B(x))Ú C(z));

в) Ø($x) (Ø"y) (A(x) ® B)) Ú C(x, y));

г) Ø("u) Ø("v)(P(u) ® Q(v) ® A(z)).

2. Встановіть, чи еквівалентні задані предикати:

а) ($х)(А(х) Ù ØВ(у))и ("z)(А(z) ® В(у));

б) ("x)((A(x) ® В(х)) Ù (А(х) ®ØВ(х))) и Ø($у) А(у).

3. Винести за дужки квантори:

а) ($ v) C(v, у)Ù (($х) А(х) Ú В);

б) ($х)($y) А(х, у) Ù ($х)($у) В(х, у);

в) ($х) А(х, у) Ú (("x) B(x)Ú ("y) С(у));

г) ($x)("y)A(x, у) Ù ($х)($z) (В(х, z) Ù ($y)A(x, у)).

4. Довести загальнозначущість таких формул:

а) ("x)P(x) ® ($y)P(y);

б) ("x)P(x) Ú (($y)ØP(y)).

5. Довести, що формула ("x)P(x) Ù ($у)ØР(у)суперечлива.

6. Довести, що формула Р(а)®Ø(($х)Р(х)) несуперечлива.

5.9. Випереджені нормальні форми і логічний висновок у логіці предикатів

Випереджена нормальна форма, алгоритм зведення до випередженої нормальної форми, правила видалення/введення квантора загальності/існування

В логіці висловлень було введено дві нормальні форми: кон'юнктивна і диз'юнктивна. В логіці предикатів вводиться третя нормальна форма, що називається випередженою нормальною формою.

Формула F в логіці предикатів знаходиться у випередженій нормальній формі (ВНФ)тоді і тільки тоді, коли вона може бути зображена у вигляді (Q₁x₁)... (Q_nx_n)(M),де кожне (Q_ix_i), і = 1, ..., п, є або ("x), або ($х), а М— формула, що не містить кванторів. Причому (Q₁x₁)... (Q_nx_n) називається префіксом,а М — матрицею формули F.

Для перетворення виразів довільної форми у ВНФ необхідно по черзі виконати такі етапи перетворення.

1. Виключити логічні зв'язки еквіваленції (~) та імплікації (®), виразивши їх через операції диз'юнкції, кон'юнкції і заперечення за допомогою таких законів:

;

.

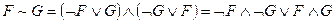2. Опустити знаки операцій заперечення безпосередньо на предикати, використовуючи закон подвійного заперечення Ø(Ø F) = F і закони де Моргана Ø(F Ú G) = ØF ÙØG, Ø(F Ù G) = ØF Ú ØG, у тому числі для кванторів:

; .

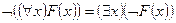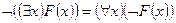3. Якщо необхідно, перейменувати зв'язані змінні.

4. Винести квантори на початок формули, використовуючи відповідні закони, для одержання випередженої нормальної форми.

Приклад.Звести формулу ("x)F(x) ® ($x)Q(x) до ВНФ.

Розв'язок. Спочатку виключимо імплікацію, потім опустимо знак операції заперечення безпосередньо на предикат і винесемо квантор на початок:

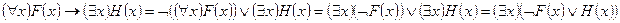
Приклад. Одержати ВНФ для формули

.

Розв'язок. Скористаємося наведеним вище алгоритмом.

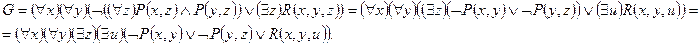
Розглянемо правила висновку, які можна використовувати для проведення дедуктивних умовиводів з висловленнями логіки предикатів, що містять квантори. Ці правила часто використовуються у ході математичних доведень без додаткового пояснення.

Правило видалення квантора загальності

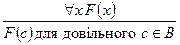
використовується для доведення істинності F(c),де с — довільно обраний елемент предметної області D, у якій справедливе "х F(x). Наприклад, із засновку «Всі студенти бажають одержувати добрі оцінки» робимо висновок: «Студент Петров бажає одержувати добрі оцінки».

Правило введення квантора загальності

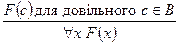
стверджує істинність "х F(x), якщо доведена істинність F(c)для будь-якого с, тобто для всіх елементів с з розглянутої предметної області D.

Правило видалення квантора існуванняв істинній формулі $х F(x)полягає в позначенні імені елемента с (конкретного або гіпотетичного), для якого F(c)істинне:

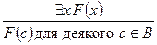
Правило введення квантора існування

дозволяє вирішити, що $х F(x)є істинним, коли відомий деякий елемент с, для якого істинне F(c).

Крім наведених правил, у логіці предикатів у ході дедуктивного висновку можна використовувати всі правила, які застосовуються для дедуктивних висновків у логіці висловлень.

Приклад.Показати, що з тверджень «Всі у першій групі вивчають математику» і «Маша — студентка першої групи» маємо висновок: «Маша вивчає математику».

Розв'язок. Позначимо через F(x)предикат «х є студент першої групи», а через М(х) — «х вивчає математику». Тоді засновки можна записати у вигляді: "х (F(x)® М(х)) і F(Маша) відповідно, а потрібний висновок — М(Маша). Для одержання цього висновку необхідно здійснити таку послідовність дій:

1. "х (F(x)® М(х)) перший засновок.

2. F(Маша)® М(Маша) крок 1, правило видалення квантора ".

3. F(Маша) другий засновок.

4. М(Маша) кроки 2 і 3, правило відділення. Таким чином, одержано шуканий результат.

Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. Ocнoвнi визначення здоров'я
5. Алгебраїчний спосіб визначення точки беззбитковості
6. Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
7. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
8. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
9. Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
10. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
11. Біостратиграфічні методи визначення віку порід
12. Біуретовий метод визначення білків

Переглядів: 1218