Завдання

1. Нехай предикат М(х, у) означає «х менше у»,предикат D(х, у)— «х дорівнює у», а предикат S(x, у, z)— «х = у + z». Наведені висловлення сформулюйте природною мовою:

а) ("x) М(0, х);

б) ("x) S(x, x, х);

в) ($x) М(х, х - 1);

г) Ø(($х) S(x, x, x));

д) ($y)($х) S(x, у, z);

e) ($y)("x) (D(х, у)Ú М(х, у));

ж)("х)("у)(S(x, у, у)® М(у, х)).

2. Нехай X — множина співробітників відділу, а Р(х), Q(x) і R(х)— предикати, що означають відповідно: х займається спортом, х вивчає іноземну мову, х має винаходи, х Î X. Розшифруйте:

а) ($х) P(x)Q(x);

б) ("x) P(x)(Q(x) ® R(x)).

3. Вказати вільні і зв'язані входження змінних у такі формули, що містять предикати А і В:

а) ("x₂) A(x₁, х₂);

б) ("x₃)(("x₁)A(x₁, х₂)¬ А(х₃, х₁);

в) ("x₂) А(х₃, х₂) ® "x₃ В(х₃, х₂);

г) ("x₂) А(x₁, х₂) ® $х₁ А(x₁, х₂);

д) ($x₂)("x₁) А(x₁, х₂)® B(х₁).

4. Задано предметну область В = {1, 2},значення констант a і b,функціональних символів f, а також предиката Р:

a	b		f(1)	f(2)		P(1,1)	P(1,2)	P(2,1)	P(2,2)

Знайти істиннісні значення таких предикатних виразів:

а) Р(а, f(a))Ù Р(b, f(.b));

б) ("x)("y)(P(x, у) ® P(f(x), f(y))).

5. Оцінити формулу ("х)(Р(х)) ® Q(f(x), а)на інтерпретації

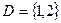
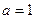
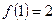
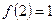Р(1)	Р(2)	Q(l,l)	Q(l,2)	Q(2,1)	Q(2,2)

5.8. Закони і тотожності у логіці предикатів

Колізія змінних, заміна зв'язаної змінної, комутативні і дистрибутивні властивості кванторів, закон де Моргана для кванторів

Всі закони і тотожності, які справедливі у логіці висловлень, залишаються справедливими і у логіці предикатів. Крім того, у логіці предикатів існують додаткові законі, що призначені для еквівалентного перетворення формул, що містять квантори та змінні.

Слід зауважити, що перенесення квантора на початок формули може змінити зміст предикатного висловлення. Так, наприклад, "х F(x)Ù "х G(x)не еквівалентне "х (F(x)Ù G(x)). У загальному випадку слід перейменувати зв'язані змінні, щоб запобігти колізії— ситуації, коли у формулі одна й та ж змінна знаходиться в області дії протилежних кванторів. Наприклад, у формулі "х (F(x))® $х (Q(x)) змінна х одночасно знаходиться в області дії кванторів " і $.

Розглянемо висловлення, що використовує предикат рівності ДОРІВНЮЄ двох чисел: "х $у ДОРІВНЮЄ(х + 1, у). Дане висловлення означає, що для будь-якого числа х існує число у, яке більше його на одиницю. Наведене висловлення є істинним. Однак, якщо поміняти порядок розташування кванторів на протилежний, то одержимо таке висловлення: $у "х ДОРІВНЮЄ(х + 1, у). Одержане висловлення означає, що існує таке число у (одне!), яке на одиницю більше будь-якого числа х. Це висловлення не відповідає попередньому і є хибним.

Для еквівалентних перетворень предикатних висловлень з кванторами необхідно використовувати наведені нижче закони. Перш ніж безпосередньо перейти до розглядання законів дій з кванторами, введемо такі позначення: .F(x) і Н(х)— одномісні предикати, Р(х, у)— двомісний предикат.

1. Заміна зв'язаної змінної:

($х) F(x)= ($у) F(y);

("x) F(x) = ("y) F(y).

Введення нового позначення зв'язаної змінної (тобто перейменування зв'язаної змінної) не змінює зміст формули логіки предикатів, якщо виконується така умова: ніяка вільна змінна у будь-якій частині формули не повинна після перейменування бути зв'язаною. Іншими словами, для нового позначення зв'язаної змінної слід обирати букву, яка відсутня у формулі. Наприклад:

("x) ($у) Р(х, у)= ("x) ($z) Р(х, z).

У даному прикладі здійснено операцію перейменування зв'язаної змінної у.

2. Комутативні властивості кванторів:

("x) ("y) Р(х, у)= ("у)("x) P(x, у);

($х) ($у) Р(х, у)= ($у) ($х) Р(х, у).

Змінювати місцями можна тільки однойменні квантори.

("x) ($у) Р(х, у) ¹ ($у) ("x) P(x, у).

3. Дистрибутивні властивості кванторів:

("x)F(x) Ú G = ("x)(F(x) Ú G);

($x)F(x) Ú G = ($x)(F(x) Ú G);

("x)F(x) Ù G = ("x)(F(x) Ù G);

($х)F(х) Ù G = ($x)(F(x) Ù G),

де G — формула логіки предикатів, яка не містить х;

("x)F(x) Ù ("x)H(x) = ("x)(F(x) Ù H(х));

($x)F(x) Ú ($х)H(х) = ($x)(F(x)Ú H(x)).

Сформульований дистрибутивний закон справедливий тільки для квантора загальності " при кон'юнкції Ù і квантора існування $ при диз'юнкції Ú, оскільки інші комбінації призводять до нерівностей:

("x)F(x) Ú ("х)H(х) ¹("x)(F(x) Ú H(х));

($x)F(x) Ù ($х)H(х) ¹ ($x)(F(x) Ù H(х)).

Для подолання цього обмеження дистрибутивного закону, слід використовувати заміну зв'язаної змінної:

("x)F(x) Ú ("х)H(х) = ("x)F(x) Ú ("у)H(у)= ("x)("y) (F(x) Ú H(y));

($x)F(x) Ù ($х)H(х) = ($x)F(x) Ù ($y)H(у)= ($х)($у) (F(x) Ù H(y)).

Таким чином, у загальному випадку дистрибутивні властивості кванторів можна записати такою схемою:

(Q₁x)F(x)Ú (Q₂y) H(у)= (Q₁x)(Q₂y) (F(x) Ú H(у));

Q₁x)F(x) Ù (Q₂y) H(у)= (Q₁x)(Q₂y) (F(x) Ù H(у)),

Де Q₁, Q₂— будь-який з кванторів $ або ".

4. Закон де Моргана для кванторів:

Ø(("x)F(x)) = ($x)ØF(x);

Ø($x)F(x)) = ("x)ØF(x).

Проілюструємо цей закон таким прикладом. Нехай предикат F(x) означає, що «х є простим числом». Коли х послідовно приймає значення ряду натуральних чисел — х = {1,2, 3, 4, 5, 6, 7, ...}, предикат відповідно змінює істиннісне значення:

F(1) = X, F(2) = I, F(3) = I;

F(4) = X, F(5) = I, F(6) = X, F(7)= I, ....

Переконаємося у справедливості першої формули для заперечення квантора загальності:

Ø(("x)F(x)) = «не всі х є простими числами» = «існують такі х, які є непростими числами» = ($х)ØF(x) = I.

Обидва наведені висловлення істинні. Тепер переконаємося у справедливості другої формули для заперечення квантора існування:

Ø(($x)F(x)) = «немає жодного х, яке було б простим» = «всіх є непростими числами» = ("x)ØF(x) = X.

Ці висловлення є хибними.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Запитання	\|	Визначення

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.