• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Дисперсії

Дисперсія посідає особливе місце у статистичному аналізі соціально-економічних явищ. На відміну від інших характеристик варіації завдяки своїм математичним властивостям вона є невіддільним і важливим елементом інших статистичних методів, зокрема дисперсійного аналізу.

Для ознак метричної шкали дисперсія — це середній квадрат відхилень індивідуальних значень ознаки від середньої:

.

Як і будь-яка середня, дисперсія має певні математичні властивості. Сформулюємо найважливіші з них.

1. Якщо всі значення варіант x_j зменшити на сталу величину А, то дисперсія не зміниться:

.

2. Якщо всі значення варіант x_j змінити в А раз, то дисперсія зміниться в A² раз:

.

3. Якщо частоти замінити частками, дисперсія не зміниться.

Нескладними алгебраїчними перетвореннями можна довести, що дисперсія — це різниця квадратів . Якщо

,

то, замінивши і поділивши всі складові на n, дістанемо:

,

де — квадрат середньої величини; — середній квадрат значень ознаки.

Дисперсія альтернативної ознаки обчислюється як добуток часток: , де — частка елементів сукупності, яким властива ознака, — частка решти елементів . Застосуємо основну формулу дисперсії до цих характеристик структури:

Якщо, скажімо, у збиральному цеху частка висококваліфікованих робітників становить , то дисперсія частки .

Дисперсія альтернативної ознаки широко використовується при проектуванні вибіркових обстежень, обробці даних соціологічних опитувань, статистичному контролі якості продукції тощо. За відсутності первинних даних про розподіл сукупності припускають, що і використовують максимальне значення дисперсії (див. підрозд. 6.4).

Якщо сукупність розбито на групи за певною ознакою х, то для будь-якої іншої ознаки у можна обчислити дисперсію як у цілому по сукупності, так і в кожній групі. Центром розподілу сукупності в цілому є загальна середня 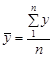, центром розподілу в j-й групі — групова середня . Відхилення індивідуальних значень ознаки у від загальної середньої можна подати як дві складові: . Узагальнюючими характеристиками цих вiдхилень є дисперсії: загальна, групова та міжгрупова.

Загальна дисперсія характеризує варіацію ознаки у навколо загальної середньої:

.

Групова дисперсія характеризує варіацію відносно групової середньої:

.

Оскільки в групи об’єднуються певною мірою схожі елементи сукупності, то варіація в групах, як правило, менша, ніж у цілому по сукупності. Якщо причинні комплекси, що формують варіацію в різних групах, неоднакові, то й групові дисперсії різняться між собою.

Узагальнюючою мірою внутрішньогрупової варіації є середня з групових дисперсій:

.

Різними є й групові середні . Мірою варіації їх навколо загальної середньої є міжгрупова дисперсія

.

Отже, загальна дисперсія складається з двох частин. Перша характеризує внутрішньогрупову, друга — міжгрупову варіацію.

Взаємозв’язок дисперсій називається правилом розкладання (декомпозиції) варіації:

.

Розглянемо розрахунок зазначених дисперсій на прикладі варіації якості твердого сиру у залежно від терміну його зберігання х. Результати вибіркового обстеження якості 20 партій сиру, розподіл їх за терміном зберігання (1, 2, 3 місяці), розрахунки середніх та дисперсій наведено в табл. 5.13. Згідно з даними таблиці маємо:

1) середній бал якості сиру (за 10-бальною шкалою)

;

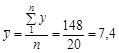2) загальна дисперсія балів якості

;

3) групові середні бали якості та групові дисперсії:

;	;
;	;
;	.

Читайте також:

1. Вибіркова дисперсія є ефективною, обгрунтованою, але ЗСУНУТОЮ точковою оцінкою для генеральної дисперсії .
2. Властивості дисперсії
3. Властивості дисперсії
4. Математичні властивості дисперсії
5. Основні властивості дисперсії.
6. Перевірка гіпотези щодо математичного сподівання при нормальному законі розподілення й невідомій дисперсії
7. Порівняння двох середніх генеральних сукупностей, дисперсії яких відомі (великі незалежні вибірки).
8. Розрахунок дисперсії

Переглядів: 2527