
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Характеристики варіації відносні (див. пит. 56)
На основі взаємозв’язку між варіаційним розмахом R, середнім квадратичним відхиленням  і чисельністю сукупності n Р. Пірсон обчислив коефіцієнти k, за допомогою яких орієнтовно можна визначити середнє квадратичне відхилення за варіаційним розмахом:
і чисельністю сукупності n Р. Пірсон обчислив коефіцієнти k, за допомогою яких орієнтовно можна визначити середнє квадратичне відхилення за варіаційним розмахом: 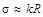 . Значення коефіцієнтів k наведено в табл. 5.5.
. Значення коефіцієнтів k наведено в табл. 5.5.
Коефіцієнти варіації
Таблиця 5.5
КОЕФІЦІЄНТИ k ДЛЯ РІЗНОГО ОБСЯГУ СУКУПНОСТІ
| n | |||||||
| k | 0,32 | 0,27 | 0,24 | 0,23 | 0,22 | 0,20 | 0,18 |
Очевидний взаємозв’язок середнього квадратичного відхилення та дисперсії:  . Дисперсія входить до більшості теорем теорії ймовірностей, які є фундаментом математичної статистики, і широко використовується для вимірювання зв’язку й перевірки статистичних гіпотез. Види та властивості дисперсій розглядаються в підрозд. 5.5.
. Дисперсія входить до більшості теорем теорії ймовірностей, які є фундаментом математичної статистики, і широко використовується для вимірювання зв’язку й перевірки статистичних гіпотез. Види та властивості дисперсій розглядаються в підрозд. 5.5.
При порівнянні варіації різних ознак або однієї ознаки в різних сукупностях використовуються коефіцієнти варіації V. Вони визначаються відношенням абсолютних іменованих характеристик варіації (  ,
,  , R) до центра розподілу, найчастіше виражаються у процентах. Значення цих коефіцієнтів залежить від того, яка саме абсолютна характеристика варіації використовується. Отже, маємо коефіцієнти варіації:
, R) до центра розподілу, найчастіше виражаються у процентах. Значення цих коефіцієнтів залежить від того, яка саме абсолютна характеристика варіації використовується. Отже, маємо коефіцієнти варіації:
лінійний  ;
;
квадратичний  ;
;
осциляції  .
.
Якщо центр розподілу поданий медіаною, то за відносну міру варіації беруть квартильний коефіцієнт варіації
 .
.
Для оцінювання ступеня варіації застосовують також співвідношення децилів. Так, коефіцієнт децильної диференціації показує кратність співвідношення дев’ятого та першого децилів:
 .
.
Необхідні для розрахунку узагальнюючих характеристик варіації величини подано в табл. 5.6 на прикладі розподілу домогосподарств за рівнем забезпеченості житлом. Середня розподілу становить 9 м2.
Таблиця 5.6
ДО РОЗРАХУНКУ УЗАГАЛЬНЮЮЧИХ ХАРАКТЕРИСТИК ВАРІАЦІЇ
| xj | fj | 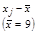
| 
| 
| 
|
| –5 | |||||
| –3 | |||||
| –1 | |||||
| Разом | ´ | ´ |
Згідно з розрахунками:
 2,53 м2;
2,53 м2;
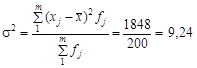 ;
;
 м2;
м2;
 .
.
Децильний коефіцієнт VD = 13,3 : 5,2 = 2,5 показує, що нижня межа 10% відносно забезпечених житлом домогосподарств в 2,5 раза перевищує верхню межу 10% малозабезпечених домогосподарств.
Читайте також:
- V. Поняття та ознаки (характеристики) злочинності
- Абсолютні і відносні величини
- Абсолютні і відносні статистичні величини
- Абсолютні і відносні швидкості
- Абсолютні й відносні посилання у формулах
- Абсолютні, відносні й змішані адреси
- Абсолютні, відносні та середні величини.
- Абсолютність і відносність практики як критерія істини.
- Акустичні характеристики порід
- Бар’єри, що базуються на перевазі (абсолютній або відносній) в рівні витрат
- БОЙОВІ ТА ТЕХНІЧНІ ХАРАКТЕРИСТИКИ СТРІЛЕЦЬКОЇ ЗБРОЇ
- Большему насыщению магнитной цепи синхронного генератора соответствует точка характеристики холостого хода
| <== попередня сторінка | | | наступна сторінка ==> |
| Дисперсії | | | Коефіцієнт локалізації |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |