• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Стандартна похибка вибірки

Стандартна похибка вибірки m є середнім квадратичним відхиленням вибіркових оцінок від значення параметра в генеральній сукупності. Як доведено в теорії вибіркового методу, дисперсія вибіркових середніх у n раз менша від дисперсії ознаки в генеральній сукупності, тобто . Оскільки на практиці генеральна дисперсія ознаки 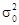невідома, у розрахунках можна використати вибіркову незсунену оцінку дисперсії: для повторної вибірки , для безповторної . Отже, формули стандартної похибки:

для повторної вибірки

,

для безповторної вибірки

.

Щодо практичного використання наведених формул слід урахувати таке:

а) дисперсія частки , де р і q — частки вибіркової сукупності, яким відповідно властива і невластива ознака;

б) у великих за обсягом сукупностях (30 і більше одиниць) поправка не вносить істотних змін у розрахунки, а тому береться до уваги лише у вибірках з невеликою кількістю елементів;

в) коригуючий множник для безповторної вибірки , тобто при малих величинах (наприклад, для 2 чи 5%-ної вибірки) наближається до 1, а тому розрахунок можна виконувати за формулою для повторної вибірки; при 10%-ній вибірці коригуючий множник становить 0,949, при 20%-ній — 0,894.

Гранична похибка вибірки — це максимально можлива похибка для взятої ймовірності F(x). Довірче число t показує, як співвідносяться гранична та стандартна похибки. Як бачимо з рис. 6.1, з імовірністю 0,683 гранична похибка не вийде за межі стандартної , з імовірністю 0,954 вона не перевищить ± 2m, з імовірністю 0,997 — ± 3m. На практиці найчастіше застосовують імовірність 0,954 (на рис. 6.1 незаштрихована частина площини).

Рис. 6.1. Співвідношення ймовірностей та ширини довірчих меж

З урахуванням сказаного формули граничних похибок середньої та частки записують так:

	Повторна вибірка	Безповторна вибірка
для середньої	;	;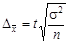
для частки	;	.

Як видно з формул, розмір граничної похибки залежить:

· від варіації ознаки s²;

· обсягу вибірки n;

· частки вибірки в генеральній сукупності ;

· узятого рівня ймовірності, якому відповідає квантиль t.

Чим більша варіація ознаки в генеральній сукупності, тим більша в середньому похибка вибірки. Залежність похибки від обсягу вибіркової сукупності обернено пропорційна. Щоб зменшити похибку вибірки вдвічі, обсяг останньої має зрости в 4 рази. При безповторному доборі похибка буде тим менша, чим більша частка обстеженої сукупності . Очевидно, при суцільному спостереженні похибка репрезентативності відсутня (D = 0).

При малих вибірках (n < 30 ), у розрахунках стандартних похибок використовують вибіркові оцінки дисперсій . Квантилі t визначають за розподілом імовірностей Стьюдента. У табл. 6.3 наведено деякі значення квантилів t розподілу Стьюдента для ймовірності 0,95 і числа ступенів свободи, тобто числа незалежних величин, необхідних для визначення даної характеристики, k = n – 1. При n > 30 квантилі розподілу Стьюдента і нормального розподілу збігаються.

Розглянемо методику вибіркового оцінювання середньої та частки на прикладі обстеження 225 домогосподарств регіону. За результатами 1%-ної вибірки 70% грошового доходу домогосподарства витрачають на харчування. Середньодушові витрати на харчування за місяць становлять 82 грн. при дисперсії 8510.

Визначимо межі середньодушових витрат на харчування з імовірністю 0,954 (t = 2).

Гранична похибка

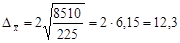грн.

Це дає підставу стверджувати з імовірністю 0,954, що середньодушові витрати на харчування в цілому по регіону щонайменше 69,7 грн. і не перевищують 94,3 грн.:

.

Перш ніж визначити граничну похибку частки витрат на харчування, необхідно обчислити її дисперсію:

= 0,7(1 – 0,7) = 0,21.

Гранична похибка

або 6,1%.

Щодо інтервалу можливих значень частки витрат на харчування в генеральній сукупності, то межі його становлять 63,9 і 76,1%:

Читайте також:

1. Абсолютна похибка наближеного
2. Види аудиторської вибірки, що застосовується в процесі внутрішнього аудиту.
3. Визначення мінімально необхідного обсягу вибірки
4. Відносна гранична похибка складе
5. Гранична похибка вибірки (див. пит. 81)
6. Довірчий інтервал характеризує точність вимірів даної вибірки, а довірча імовірність – достовірність виміру.
7. Лекція 10 Числові характеристики вибірки. Статистична функція розподілу
8. Лекція 9 Завдання математичної статистики. Генеральна сукупність і вибі­рка. Варіаційний ряд. Графічне зображення вибірки
9. Методика формування обсягу вибірки в процесі маркетингових досліджень
10. Міжнародна стандартна торговельна класифікація (SІТС).
11. Мінімальна стандартна модель Світового банку для оцінки зовнішньоборгової залежності держави
12. Мінімально необхідні обсяги вибірки

Переглядів: 8710