
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Основні поняття та визначення

| На рис. 12а наведено шарнірно обперту балку – геометрично незмінювану систему.
Всі три реакції  визначаються з трьох умов рівноваги плоскої системи сил.
визначаються з трьох умов рівноваги плоскої системи сил.
|
Використовуючи метод перерізів, легко знайти внутрішні силові фактори у будь якому перерізі балки.
Додамо ще одну шарнірну - рухому опору в перерізі С (рис. 12б). У наслідок цього система стала більш міцною та жорсткою, проте з погляду геометричної незмінюваності цей зв’язок зайвий. Тепер з трьох рівнянь рівноваги чотири реакції  визначити неможливо. Балка, що зображена на рис. 12б, один раз статично невизначувана, т. я. реакції зв’язків не можуть бути однозначно визначені з рівнянь статичної рівноваги.
визначити неможливо. Балка, що зображена на рис. 12б, один раз статично невизначувана, т. я. реакції зв’язків не можуть бути однозначно визначені з рівнянь статичної рівноваги.
Таким чином, статично невизначуваними називаються системи, силові фактори в елементах яких тільки з рівнянь рівноваги визначити неможна. У таких системах зв’язків більше, ніж необхідно для рівноваги. Отже, деякі зв’язки виявляються в цьому розумінні так би мовити зайвими, а зусилля в них – зайвими невідомими. За числом зайвих зв’язків або зайвих невідомих зусиль установлюють ступінь статичної невизначуваності системи.
Ступінню статичної невизначуваності системи  називається різниця між числом невідомих зусиль та кількістю незалежних рівнянь статичної рівноваги, які можна записати для даної системи.
називається різниця між числом невідомих зусиль та кількістю незалежних рівнянь статичної рівноваги, які можна записати для даної системи.
Положення жорсткого стержня в просторі визначається шістьма незалежними координатами, інакше кажучи, жорсткий стержень володіє шістьма ступенями свободи. На стержень можуть бути накладені зв'язки, тобто обмеження, що обумовлюють його певне положення в просторі. Найбільш простими зв'язками є такі, при яких повністю виключаються те або інше узагальнене переміщення для деяких перерізів стержня. Накладення одного зв'язку знімає одну ступінь свободи з стержня як жорсткого цілого. Отже, якщо на вільний жорсткий стержень накладено шість зовнішніх зв'язків, то положення його в просторі як жорсткого цілого буде, за деякими виключеннями, визначено повністю і система з механізму, що володіє шістьма ступенями свободи, перетворюється в кінематично незмінну систему. Те число зв'язків, при якому досягається кінематична незмінність, носить назву необхідного числа зв'язків. Всякий зв'язок, накладений зверх необхідних, називають додатковим. Число додаткових зв'язків дорівнює ступеню статичної невизначуваності системи.
Зв'язки в рамах і стержньових системах ділять звичайно на зв'язки зовнішні і зв'язки внутрішні, або взаємні. Під зовнішніми зв'язками розуміються умови, що накладаються на абсолютні переміщення деяких точок системи. В разі плоскої системи у шарнірно - рухомій опорі є один зовнішній зв'язок, в нерухомому шарнірі - два, в жорсткому закріпленні - три. Просторове закріплення відповідає шести зовнішнім зв'язкам. Зовнішні зв'язки часто ділять на необхідні і додаткові. Наприклад, на рис.13а,б показана плоска рама, що має в першому випадку три зовнішні зв'язки, а у другому п'ять зовнішніх зв'язків.

|
Для того щоб визначити положення рами в площині як жорсткого цілого, необхідне накладення трьох зв'язків. Отже, в першому випадку рама має необхідні зовнішні зв'язки, а у другому, крім того, два додаткові зовнішні зв'язки.
Під внутрішніми, або взаємними, зв'язками розуміються обмеження, що накладаються на взаємні зміщення елементів рами. Тут також можна говорити як про необхідні, так і про додаткові зв'язки.

| Так, наприклад, плоска рама, показана на рис. 14а, має необхідну кількість як зовнішніх, так і внутрішніх зв'язків між елементами. Це кінематично незмінна система. |
Якщо будуть задані зовнішні сили, ми зможемо за допомогою рівнянь статики знайти як реакції опор, так і внутрішні силові фактори в будь-якому поперечному перерізі рами. У тій же рамі, показаній на рис. 14б, крім зовнішніх накладені два додаткові внутрішні зв'язки, які забороняють взаємне вертикальне і горизонтальне зміщення точок А і В. Система в цьому випадку двічі статично невизначувана (іноді додають: “внутрішнім образом"). У рамі рис. 13а,б також є внутрішні додаткові зв'язки. Контур рами повністю замкнутий. Розрізаючи його в будь-якому перерізі (рис. 15), ми, не порушуючи кінематичної незмінюваності, отримуємо можливість при заданих силах знайти внутрішні силові фактори в кожному перерізі рами.

| Отже, розрізаючи замкнену раму, ми знімаємо додаткові зв'язки, тобто дозволяємо перетинам А і В повертатися і зміщуватися в двох напрямках один відносно одного. |
Узагальнюючи, можна сказати, що замкнений плоский контур має три додаткові внутрішні взаємні зв’язки. Таким чином, рама, показана на рис. 13а, тричі статично невизначувана. Рама показана на рис. 13б, п'ять разів статично невизначувана (три рази внутрішнім образом і два рази – зовнішнім).

| Статична невизначуваність може бути наслідком не тільки введення додаткової зовнішніх зв’язків, а й з умов утворення системи. Розглянемо раму, показану на рис. 16а. Очевидно, що реакції  зовнішніх зв’язків (опор) легко визначити з рівнянь рівноваги. зовнішніх зв’язків (опор) легко визначити з рівнянь рівноваги.
|
Проте після цього рівняння рівноваги не дають змоги визначити всі силові фактори в елементах рами.
Розріжемо раму на дві частини й розглянемо рівновагу однієї з частин (рис. 16б). Дію відкинутої частини на залишену замінимо в кожному з перерізів розрізу трьома внутрішніми силовими факторами: осьовою силою 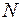 , поперечною силою
, поперечною силою 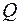 та згинальним моментом
та згинальним моментом  . Отже, з трьох рівнянь рівноваги треба визначити дев’ять невідомих зусиль. Система шість разів статично невизначувана. Вона складається з двох замкнених безшарнірних контурів. Кожний замкнений контур тричі статично невизначуваний.
. Отже, з трьох рівнянь рівноваги треба визначити дев’ять невідомих зусиль. Система шість разів статично невизначувана. Вона складається з двох замкнених безшарнірних контурів. Кожний замкнений контур тричі статично невизначуваний.
Читайте також:
- A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
- CMM. Визначення моделі зрілості.
- I визначення впливу окремих факторів
- I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- II. Основні засоби
- II. ОСНОВНІ ПОВНОВАЖЕННЯ ТРУДОВИХ КОЛЕКТИВІВ
- II. Поняття соціального процесу.
- II.3. Основні способи і прийоми досягнення адекватності
- III. Основні обов'язки робітників та службовців
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Метод сил |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |