
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Функція розподілу ймовірностей (інтегральна функція) та її властивості
Закон розподілу ймовірностей можна подати ще в одній формі, яка придатна і для дискретних, і для неперервних випадкових величин, а саме: як функцію розподілу ймовірностей випадкової величини F(х), так звану інтегральну функцію.
Функцію аргументу х, що визначає ймовірність випадкової події Х < x, називають функцією розподілу ймовірностей:
F(x) = P(X < x) (62)
Цю функцію можна тлумачити так: унаслідок експерименту випадкова величина може набути значення, меншого за х .
Розглянемо властивості F(x):
1. 
Ця властивість випливає з означення функції розподілу.
2. 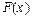 є неспадною функцією, а саме
є неспадною функцією, а саме 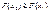 , якщо
, якщо 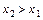 .
.
| ! |
Доведення.Позначимо відповідно А, В, С події (Х < x2), (Х < x1) і 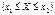 . Випадкові події В і С є несумісними (А
. Випадкові події В і С є несумісними (А 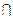 С = Æ) / Тоді подію А можна записати так:
С = Æ) / Тоді подію А можна записати так:
А = В 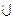 С (А = В + С).
С (А = В + С).
За формулою додавання для несумісних випадкових подій (6) маємо:
Р(А) = Р(В 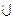 С) = Р(В) + Р(С)
С) = Р(В) + Р(С)
або
Р(Х < x2) = Р(Х < x1) + P(x1 £ Х £ х2). (63)
Звідси на підставі означення інтегральної функції F(x), дістаємо
F(x2) = F(x1) + P(x1 £ Х £ х2)
або
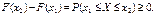 (64)
(64)
Отже,

Із другої властивості F(x) випливають наведені далі висновки:
1. Імовірність того, що випадкова величина Х набуде можливого значення  , дорівнює приросту інтегральної функції F(x) на цьому проміжку:
, дорівнює приросту інтегральної функції F(x) на цьому проміжку:
 (65)
(65)
2. Якщо випадкова величина Х є неперервною, то ймовірність того, що вона набуде конкретного можливого значення, завжди дорівнює нулю:
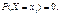
І справді, поклавши в (65) 
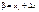 , дістанемо
, дістанемо
 .
.
Коли 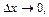 маємо:
маємо:
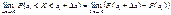 . (66)
. (66)
Оскільки при  Х = хі, то
Х = хі, то

що й потрібно було довести.
Отже, для неперервної випадкової величини Х справджуються такі рівності:
 (67)
(67)
3. Якщо  , виконуються два подані далі співвідношення.
, виконуються два подані далі співвідношення.
1) 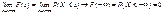
Оскільки подія Х < – ¥ полягає в тому, що випадкова величина набуває значення, яке міститься ліворуч від – ¥. А така подія є неможливою (Æ).
2) 
Подія Х <  полягає в тому, що випадкова величина Х набуває числового значення, яке міститься ліворуч від + ¥. Ця подія є віро-
полягає в тому, що випадкова величина Х набуває числового значення, яке міститься ліворуч від + ¥. Ця подія є віро-
гідною (Ώ), оскільки будь-яке число X = x <  .
.
Із цих двох співвідношень випливає висновок: якщо можливі значення випадкової величини Х належать обмеженому проміжку [а; b], то

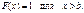 (68)
(68)
Приклад 6.Закон розподілу дискретної випадкової величини Х задано таблицею:
| Х = хі | – 4 | – 1 | ||||
| Р(Х = хі) = рі | 0,1 | 0,2 | 0,1 | 0,3 | 0,1 | 0,2 |
Побудувати F(x) та її графік.
Розв’язання. Згідно з властивостями F(x), дістаємо наведені далі співвідношення.
1) F(– 4) = P(X < – 4) = 0;
2) F(–1) = P(X < –1) = P(X = – 4) = 0,1;
3) F(2) = P(X < 2) = P(X = – 4) + P(X = –1) = 0,1 + 0,2 = 0,3;
4)F(6) = P(X < 6) = P(X = – 4) + P(X = –1) + P(X = 2) = 0,1 + 0,2 +
+ 0,1 = 0,4;
5) F(9) = P(X < 9) = P(X = – 4) + P(X = –1) + P(X = 2) + P(X = 6) =
= 0,1 + 0,2 + 0,1 + 0,3 = 0,7;
6) F(12) = P(X < 13) = P(X = – 4) + P(X = –1) + P(X = 2) + P(X = 9) =
= 0,1 + 0,2 +0,1 + 0,3 + 0,1 = 0,8;
7) F(x)|x >13 = P(X > 13) = P(X = – 4) + P(X = –1) + P(X = 2) + P(X = 9) +
+ P(X = 13) = 0,1 + 0,2 +0,1 + 0,1 + 0,3 + 0,1 + 0,2 = 1.
Компактно F(x) можна записати в такій формі: 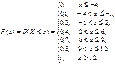
Графік функції F(x) зображено на рис. 23.

Рис. 23
22. Щільність імовірностей (диференціальна функція) f(x) і її властивості
Для неперервних випадкових величин закон розподілу ймовір-
ностей зручно описувати з допомогою щільності ймовірностей, яку позначають f (x).
Щільністю ймовірностей неперервної випадкової величини Х називається перша похідна від інтегральної функції F(x):
 (69)
(69)
звідки 
Оскільки

то добуток f (x) dx — ймовірність того, що випадкова величина Х міститиметься у проміжку [х, х + dx], де 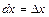 .
.
Геометрично на графіку щільності ймовірності f (x) dx відповідає площа прямокутника з основою dx і висотою f (x) (рис. 27а).
 Рис. 27а
Рис. 27а
Властивості f (x)
1.  . Ця властивість випливає з означення щільності ймовірності як першої похідної від F(x) за умови, що F(x) є неспадною функцією.
. Ця властивість випливає з означення щільності ймовірності як першої похідної від F(x) за умови, що F(x) є неспадною функцією.
2. Умова нормування неперервної випадкової величини Х:
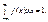 (70)
(70)
| ! |
Доведення. 
Якщо неперервна випадкова величина Х визначена лише на проміжку [a; b], то умова нормування має такий вигляд:  (71)
(71)
3. Імовірність попадання неперервної випадкової величини в інтервалі  обчислюється за формулою
обчислюється за формулою
| ! |
 (72)
(72)
Доведення. За властивістю функції розподілу ймовірностей (67)
 Залежність (72) можна подати так:
Залежність (72) можна подати так:

4. Функція розподілу ймовірностей неперервної випадкової величини має вигляд
 (73)
(73)
| ! |
Доведення.  .
.
Якщо можливі значення неперервної випадкової величини належать лише інтервалу [а; b], то 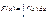 (74)
(74)
Приклад 2. Закон неперервної випадкової величини Х задано у вигляді:

Знайти F(x) і побудувати графіки функцій f (x), F(x). Обчислити
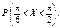
Розв’язання.Згідно із (74) маємо:
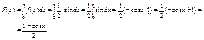
Отже, функція розподілу ймовірностей буде така:

Графіки функцій f (x), F(x) зображені відповідно на рис. 29 і 30.
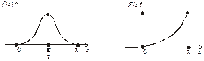
Рис. 29 Рис. 30
Імовірність події 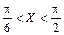 можна обчислити згідно з (65) або (72). Застосуємо формулу (72):
можна обчислити згідно з (65) або (72). Застосуємо формулу (72):

Читайте також:
- I. Доповнення до параграфу про точкову оцінку параметрів розподілу
- Overall Reflection Properties - Загальні Властивості Віддзеркалення
- OПТИЧНІ ВЛАСТИВОСТІ КОЛОЇДНИХ СИСТЕМ
- VII розділ. Маркетингові рішення з розподілу та збуту товару
- А) Товар і його властивості.
- Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
- Автоматизація водорозподілу з комбінованим регулюванням
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Автоматизація водорозподілу регулювання зі сталими перепадами
- Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
- Автоматизація водорозподілу регулюванням за верхнім б'єфом
- Автоматизація водорозподілу регулюванням за нижнім б'єфом
| <== попередня сторінка | | | наступна сторінка ==> |
| Формула Пуассона | | | Математичне сподівання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |