
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Формула Пуассона
Імовірність того, що за проміжок часу t +  не відбудеться жодна подія, подається у вигляді:
не відбудеться жодна подія, подається у вигляді:

 (52)
(52)
Імовірність того, що за цей самий проміжок часу здійсниться m подій, визначається так:
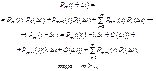
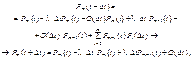 (53)
(53)
оскільки  .
.
Перенісши  і
і  в рівняннях (52), (53) у ліву частину, дістанемо таку систему рівнянь:
в рівняннях (52), (53) у ліву частину, дістанемо таку систему рівнянь:
 (54)
(54)
Поділимо ліву і праву частини системи рівнянь (54) на 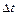 і виконаємо граничний перехід при
і виконаємо граничний перехід при  . У результаті дістанемо систему лінійних диференціальних рівнянь:
. У результаті дістанемо систему лінійних диференціальних рівнянь:
 ;
;
 . (55)
. (55)
Для розв’язування системи (55) використаємо твірну функцію
 . (56)
. (56)
Розглянемо властивості функції А(х, t). При х = 1 А(1, t) = 1.
При х = 0 А(0, t) = p0(t), А(х, 0) = р0 (0) = 1,
 . (57)
. (57)
Помножимо друге рівняння системи (55) на хm і підсумуємо ліву та праву частини рівняння:
 .
.
або з урахуванням (56)
 . (58)
. (58)
Розв’язавши диференціальне рівняння, дістанемо:
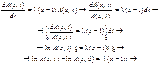
 , (59)
, (59)
оскільки А(х, 0) = р0(0) = 1.
Згідно з властивістю А(x, t) маємо:
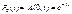 ;
;
 .
.
Отже, імовірність того, що за час t відбудеться m випадкових подій, які утворюють найпростіший потік, обчислюється за формулою
 , (60)
, (60)
де  — це інтенсивність найпростішого потоку, тобто: середнє число подій, які відбудуться за одиницю часу [с, хв, год].
— це інтенсивність найпростішого потоку, тобто: середнє число подій, які відбудуться за одиницю часу [с, хв, год].
Приклад. Автомобілі, що рухаються по шосе в одному напрямку, утворюють найпростіший потік із параметром  (тобто, через умовну лінію, яка проведена перпендикулярно до шосе в певному місці, у середньому проїжджає 3 автомобілі за 1 с. Обчислити ймовірність того, що за 2 с через умовну лінію проїде: 1) 4 автомобілі; 2) не більш як 4.
(тобто, через умовну лінію, яка проведена перпендикулярно до шосе в певному місці, у середньому проїжджає 3 автомобілі за 1 с. Обчислити ймовірність того, що за 2 с через умовну лінію проїде: 1) 4 автомобілі; 2) не більш як 4.
Розв’язання. Із умови задачі: 
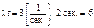 .
.
За таблицею (дод. 3), коли 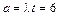 знаходять:
знаходять:
1)  ;
;
2) 
= 
Формула Пуассона для малоймовірних
випадкових подій
Точність асимптотичних формул для великих значень n — числа повторних незалежних експериментів за схемою Бернуллі — знижується з наближенням p до нуля. Тому при 
 за умови np = a =const імовірність появи випадкової події m раз
за умови np = a =const імовірність появи випадкової події m раз  обчислюється за такою асимптотичною формулою:
обчислюється за такою асимптотичною формулою:
 , (47)
, (47)
яка називається формулою Пуассона.
| ! |
Доведення. Оскільки а = np, то 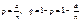 .
.
Запишемо формулу Бернуллі у такому вигляді:





Коли  , дістаємо:
, дістаємо:

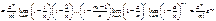 .
.
Оскільки  ,
,
 .
.
Отже,
 ,
,
а для великих, але обмежених значень n маємо:
 , що й потрібно було довести.
, що й потрібно було довести.
Із (47) випливає:
 ; (48)
; (48)
 .
.
І справді, це підтверджується ще й тим, що події  утворюють повну групу.
утворюють повну групу.
Функція Рn (m) визначається за таблицею, наведеною в дод. 3, за заданим m і обчисленим значенням а = np.
Приклад 1. Радіоприлад містить 1000 мікроелементів, які працюють незалежно один від одного, причому кожний може вийти з ладу під час роботи приладу з імовірністю р =
= 0,002. Обчислити ймовірності таких випадкових подій:
1) під час роботи приладу з ладу вийдуть 3 мікроелементи; 2) від трьох до шести.
Розв’язання. За умовою задачі маємо n = 1000; p = 0,002; m = 3; 3  . Оскільки n велике, а р мале число, то для обчислення ймовірностей застосуємо формули (47) і (48). Для цього обчислимо значення параметра а = np = 1000 · 0,002 = 2.
. Оскільки n велике, а р мале число, то для обчислення ймовірностей застосуємо формули (47) і (48). Для цього обчислимо значення параметра а = np = 1000 · 0,002 = 2.
1)  .
.
2) 

20.Дискретні та неперервні випадкові величини.
Закони розподілу їх імовірностей
Розглянемо такий простір елементарних подій, в якому кожній елементарній події 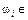 Ώ відповідає одне і лише одне число х або набір чисел
Ώ відповідає одне і лише одне число х або набір чисел 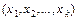 , тобто на множині Ώ визначена певна функція
, тобто на множині Ώ визначена певна функція  , яка кожній елементарній події
, яка кожній елементарній події  ставить у відповідність певний елемент одновимірного простору R1 або n-вимірного простору Rn.
ставить у відповідність певний елемент одновимірного простору R1 або n-вимірного простору Rn.
Цю функцію називають випадковою величиною. У разі, коли 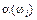 відображає множину Ώ на одновимірний простір R1, випадкову величину називають одновимірною. Якщо відображення здійснюється на Rn, то випадкову величину називають n-вимірною (системою n випадкових величин або n-вимірним випадковим вектором).
відображає множину Ώ на одновимірний простір R1, випадкову величину називають одновимірною. Якщо відображення здійснюється на Rn, то випадкову величину називають n-вимірною (системою n випадкових величин або n-вимірним випадковим вектором).
Схематично одновимірну випадкову величину унаочнює рис. 19.
 Рис. 19
Рис. 19
Отже, величина називається випадковою, якщо внаслідок проведення експерименту під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю.
Якщо множина можливих значень випадкової величини є зчисленною то таку величину називають дискретною. У противному разі її називають неперервною.
Приклад 1. Задано множину цілих чисел Ώ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Навмання беруть одне число. Елементарними подіями будуть такі: поява одного з чисел  1, 2, 3, …,10 з певною ймовірністю. Множина можливих значень
1, 2, 3, …,10 з певною ймовірністю. Множина можливих значень  є дискретною, а тому й випадкова величина — поява одного з чисел множини Ώ — буде дискретною.
є дискретною, а тому й випадкова величина — поява одного з чисел множини Ώ — буде дискретною.
Випадкові величини позначають великими літерами латинського алфавіту X, Y, Z, ... , а їх можливі значення — малими х; у; z, ... .
Для опису випадкової величини необхідно навести не лише множину можливих її значень, а й указати, з якими ймовірностями ця величина набуває того чи іншого можливого значення.
З цією метою вводять поняття закону розподілу ймовірностей.
Співвідношення, що встановляє зв’язок між можливими значеннями випадкової величини та відповідними їм імовірностями, називають законом розподілу випадкової величини.
Закон розподілу дискретної випадкової величини Х можна задати в табличній формі або за допомогою ймовірнісного многокутника.
У разі табличної форми запису закону подається послідовність можливих значень випадкової величини Х, розміщених у порядку зростання, та відповідних їм імовірностей:
| Х = хі | х1 | х2 | х3 | ...... | хk |
| Р(Х = хі) = рі | р1 | р2 | р3 | ..... | рk |
Оскільки випадкові події (Х = хj) і (Х = хm) є між собою несумісними ((Х = хі) ∩ (Х = хm) = Æ, і 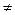 m; і, m = 1, 2, …, k) і утворюють повну групу
m; і, m = 1, 2, …, k) і утворюють повну групу  , то необхідною є така умова:
, то необхідною є така умова:
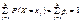 (61)
(61)
Рівність (61) називають умовою нормування для дискретної випадкової величини Х. Наведену таблицю називають рядом розподілу.
| Х = хі | –4 | ||||
| Р(Х = хі) = рі | 0,1 | 0,1 | 0,5 | р4 | 0,2 |
Приклад 3. Закон розподілу дискретної випадкової величини Х задано таблицею
Знайти ймовірність можливого значення випадкової величини Х = х4 = 5.Розв’язання. Згідно з умовою нормування (61) маємо:

Читайте також:
- I. Формула спеціальності
- I. Формула спеціальності
- I. Формула спеціальності
- Абсолютні й відносні посилання у формулах
- Барометрична формула
- Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
- Вступне звернення і заключна формула ввічливості
- Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.
- Грування, тобто має місце формула
- Загальна формула для визначення переміщень. Метод Мора
- Загальна формула руху капіталу
- Зв'язок невизначеного і визначеного інтегралів. Формула Ньютона-Лейбніца.
| <== попередня сторінка | | | наступна сторінка ==> |
| Використання інтегральної теореми | | | Функція розподілу ймовірностей (інтегральна функція) та її властивості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |