
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Конус. Осьовий переріз конуса. Перерізи конуса площинами.
Конус – це тіло, що складається з круга, точки, що не лежить на площині круга, та відрізків, що сполучають дану точку з точками круга.
Конус – тіло, утворене обертанням прямокутного трикутника навколо одного із його катетів.
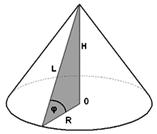
Основою конуса є круг, вершиною конуса є точка, що не лежить у площі круга, твірними конуса є відрізки, що сполучають вершину конуса з точками кола основи.
Прямим є конус, у якого пряма, що сполучає вершину конуса з центром його основи, перпендикулярна до площини основи. Висотою конуса є перпендикуляр, опущений з вершини на площу основи.
Віссю прямого конуса є пряма, що містить його висоту.
Площина, паралельна основі прямого конуса, перетинає конус по кругу, а бічну поверхню по колу з центром на осі конуса.
Якщо січна площина проходить через вісь конуса, то його переріз – це рівнобедрений трикутник, основа якого дорівнює діаметру основи конуса, а бічні сторони є твірними конуса. Такий переріз називається осьовим.

 Конус, осьовий переріз якого є рівностороннім трикутником, називається рівностороннім конусом. Якщо січна площина проходить через вершину конуса під кутом до площини основи, то його переріз – це рівнобедрений трикутник, основа якого є хордою основи конуса, а бічні сторони – твірними конуса.
Конус, осьовий переріз якого є рівностороннім трикутником, називається рівностороннім конусом. Якщо січна площина проходить через вершину конуса під кутом до площини основи, то його переріз – це рівнобедрений трикутник, основа якого є хордою основи конуса, а бічні сторони – твірними конуса.
Якщо січна площина проходить паралельно основі конуса, то перерізом є круг з центром на осі конуса. Така січна площина розтинає конус на дві частини – конус і зрізаний конус. Круги, що лежать у паралельних площинах цього конуса, – його основи; відрізок, що з’єднує їх центри, - це висота зрізаного конуса.
Дотичною площиною до конуса називається площина, що проходить через твірну конуса і перпендикулярна площині осьового перерізу, яка містить цю твірну.
Конус.
 - площа бічної поверхні конуса.
- площа бічної поверхні конуса.
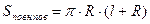 - площа повної поверхні конуса.
- площа повної поверхні конуса.
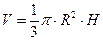 - об’єм конуса.
- об’єм конуса.
Розв’язання задач, підготовка до письмової роботи
до теми«Площі поверхонь та об’єм конуса».
№ 1.
Дано конус. Твірна = 15 см, а діаметр основи = 18 см.
Знайти:
1) S осьового перерізу; 2) S основи; 3) S бічної поверхні; 4) S повної поверхні; 5) V конуса.

Дано конус, l = АS = 15 см, АВ = 18 см.
Знайти: 1)  - ? 2)
- ? 2)  -? 3)
-? 3)  -? 4)
-? 4)  -? 5)
-? 5) 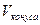 -?
-?
Розв’язання:
1)  - ?
- ?
Осьовим перерізом конуса є рівнобедрений трикутник АSВ. АS = ВS. Його площу знайдемо за формулою: 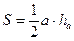 .
. 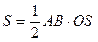 ; ОS - ?
; ОS - ?
З D АОS (ÐО = 90°) за теоремою Піфагора обчислимо ОS.

 Н = ОS = 12 см.
Н = ОS = 12 см.
Обчислимо  .
. 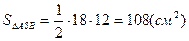 ,
,  = 108 см2.
= 108 см2.
2)  -?
-?
Основою конуса є круг, його площа знаходиться за формулою: 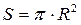 .
.
Обчислимо 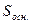 . R =
. R = 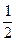 АВ =
АВ =  ×18 = 9 (см),
×18 = 9 (см),  .
.  = 81p см2.
= 81p см2.
3)  -?
-?
 ;
;  ;
;  = 135p см2.
= 135p см2.
4)  -?
-?
 ;
;  ;
;  = 216p см2.
= 216p см2.
5) 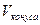 -?
-?
Для знаходження об’єму конуса скористаємося формулою: 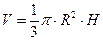 .
.
Обчислимо 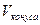 .
.  (см3),
(см3), 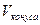 = 324 p см3.
= 324 p см3.
Відповідь:
-
 = 108 см2.
= 108 см2. -
 = 81p см2.
= 81p см2. -
 = 135p см2.
= 135p см2. -
 = 216p см2.
= 216p см2. -
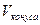 = 324 p см3.
= 324 p см3.
№ 2.
Дано конус. Висота конуса = 4 см, а довжина кола основи = 6p см.
Знайти:
1) S осьового перерізу; 2) S основи; 3) S бічної поверхні; 4) S повної поверхні; 5) V конуса.
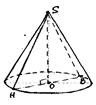 Дано конус, Н = ОS = 4 см, с = 6p см.
Дано конус, Н = ОS = 4 см, с = 6p см.
Знайти: 1)  - ? 2)
- ? 2)  -? 3)
-? 3)  -? 4)
-? 4)  -? 5)
-? 5) 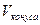 -?
-?
Розв’язання:
1)  - ?
- ?
Осьовим перерізом конуса є рівнобедрений трикутник АSВ. АS = ВS. Його площу знайдемо за формулою: 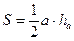 .
.  ; АВ - ?
; АВ - ?
АВ = 2 АО = 2R, R - ?
За умовою: с = 6p см. За формулою:  .
.
с = с, 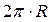 = 6p , R = 3 см, тоді АВ = 2×3 = 6(см), АВ = 6 см.
= 6p , R = 3 см, тоді АВ = 2×3 = 6(см), АВ = 6 см.
Обчислимо  .
.  ,
, 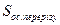 =12 см2.
=12 см2.
2) 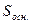 -?
-?
Основою конуса є круг, його площа знаходиться за формулою: 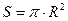 .
.
Обчислимо 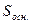 ,
, 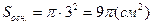 .
. 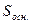 = 9p см2.
= 9p см2.
3)  -?
-?
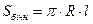 , l = АS - ?
, l = АS - ?
З D АОS (ÐО = 90°) за теоремою Піфагора обчислимо АS.

 l = АS = 5 см.
l = АS = 5 см.
Обчислимо  .
.  ,
,  = 15p см2.
= 15p см2.
4)  -?
-?
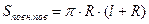 ;
; 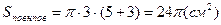 ;
;  = 24p см2.
= 24p см2.
5) 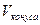 -?
-?
Для знаходження об’єму конуса скористаємося формулою: 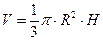 .
.
Обчислимо 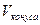 .
. 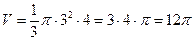 (см3),
(см3), 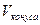 = 12p см3.
= 12p см3.
Відповідь:
-
 = 12 см2.
= 12 см2. -
 = 9p см2.
= 9p см2. -
 = 15p см2.
= 15p см2. -
 = 24p см2.
= 24p см2. -
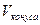 = 12p см3.
= 12p см3.
№ 3.
Дано конус. Кут нахилу твірної до основи = 30°. Твірна = 12 см.
Знайти:
1) S осьового перерізу; 2) S основи; 3) S бічної поверхні; 4) S повної поверхні; 5) V конуса.
Дано конус, l = АS = 12 см, ÐSАО = 30°.
 Знайти: 1)
Знайти: 1)  - ? 2)
- ? 2)  -? 3)
-? 3)  -? 4)
-? 4)  -? 5)
-? 5) 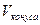 -?
-?
Розв’язання:
1)  - ?
- ?
Осьовим перерізом конуса є рівнобедрений трикутник АSВ. АS = ВS. Його площу знайдемо за формулою: 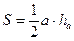 .
. 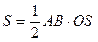 ; АВ - ? ОS - ?
; АВ - ? ОS - ?
З D АОS (ÐО = 90°) за співвідношенням кутів та сторін в прямокутному трикутнику обчислимо ОS і АО: sin ÐА =  Þ
Þ 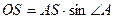 ;
;  , Н = ОS = 6 см.
, Н = ОS = 6 см.
cosÐА =  Þ
Þ 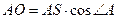 ;
; 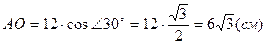 . АО = R =
. АО = R = 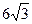 см.
см.
Довжину АО можна знайти іншим способом: через tg ÐA, або ctgÐA, або за теоремою Піфагора.
АВ = 2×R = 2× 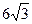 =
=  (см)
(см)
Обчислимо  .
.  ,
,  =
= 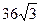 см2.
см2.
2) 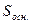 -?
-?
Основою конуса є круг, його площа знаходиться за формулою: 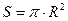 .
.
Обчислимо 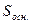 ,
, 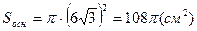 .
.  = 108p см2.
= 108p см2.
3)  -?
-?
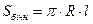 ;
; 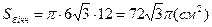 ;
;  =
=  p см2.
p см2.
4)  -?
-?
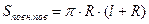 ;
;  ;
;
 =
=  p см2.
p см2.
5) 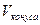 -?
-?
Для знаходження об’єму конуса скористаємося формулою: 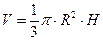 .
.
Обчислимо 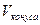 .
.  (см3),
(см3), 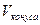 = 216p см3.
= 216p см3.
Відповідь:
-
 =
= 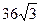 см2.
см2. -
 = 108p см2.
= 108p см2. -
 =
=  p см2.
p см2. -
 =
=  p см2.
p см2. -
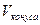 = 216p см3.
= 216p см3.
№ 4.
Дано конус. Кут нахилу твірної до висоти = 60°. Твірна = 8см.
Знайти: 1) S осьового перерізу; 2) S основи; 3) S бічної поверхні; 4) S повної поверхні; 5) V конуса.
Дано конус, l = АS = 8 см, ÐАSО = 60°.
Знайти: 1)  - ? 2)
- ? 2)  -? 3)
-? 3)  -? 4)
-? 4)  -? 5)
-? 5) 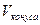 -?
-?
 Розв’язання:
Розв’язання:
1)  - ?
- ?
Осьовим перерізом конуса є рівнобедрений трикутник АSВ. АS = ВS. Його площу знайдемо за формулою: 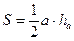 .
. 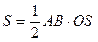 ; АВ - ? ОS - ?
; АВ - ? ОS - ?
З D АОS (ÐО = 90°) маємо, що ÐSАО = 30°, тому ОS = 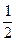 АS =
АS =  × 8 = 4(см), (катет, що лежить навпроти кута 30° дорівнює
× 8 = 4(см), (катет, що лежить навпроти кута 30° дорівнює  гіпотенузи.) Н = 4 см.
гіпотенузи.) Н = 4 см.
З D АОS (ÐО = 90°) за теоремою Піфагора обчислимо АО:

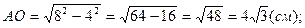 R=
R= 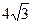 см
см
АВ = 2 АО = 2× 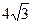 =
= 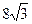 (см). Обчислимо
(см). Обчислимо  .
. 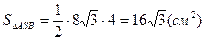 ,
,  =
= 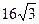 см2.
см2.
2)  -?
-?  .
.
Обчислимо 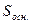 ,
, 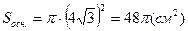 .
.  = 48p см2.
= 48p см2.
3)  -?
-?
 ;
; 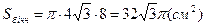 ;
;  =
= 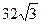 p см2.
p см2.
4)  -?
-?
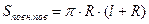 ;
;  ;
;
 =
=  p см2.
p см2.
5) 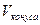 -?
-?
Для знаходження об’єму конуса скористаємося формулою: 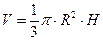 .
.
Обчислимо 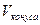 .
.  (см3),
(см3), 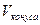 = 64p см3.
= 64p см3.
Відповідь:
-
 =
= 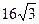 см2.
см2. -
 = 48p см2.
= 48p см2. -
 =
=  p см2.
p см2. -
 =
=  p см2.
p см2. -
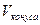 = 64p см3.
= 64p см3.
Письмова робота до теми«Площі поверхонь та об’єм конуса».
І варіант.
1. Дано конус. Твірна = 10 см, а довжина кола основи = 12p см.
Знайти: 1) S осьового перерізу; 2) S основи; 3) S бічної поверхні; 4) S повної поверхні; 5) V конуса.
2. Дано конус. Кут нахилу твірної до основи = 30°. Твірна = 10 см.
Знайти: 1) S осьового перерізу; 2) S основи; 3) S бічної поверхні; 4) S повної поверхні; 5) V конуса.
ІІ варіант.
1. Дано конус. Висота конуса = 16 см, а діаметр основи = 24 см.
Знайти: 1) S осьового перерізу; 2) S основи; 3) S бічної поверхні; 4) S повної поверхні; 5) V конуса.
2. Дано конус. Кут нахилу твірної до висоти = 60°. Твірна = 10 см.
Знайти: 1) S осьового перерізу; 2) S основи; 3) S бічної поверхні; 4) S повної поверхні; 5) V конуса.
Читайте також:
- А АА1В1В – осьовий переріз
- Вибір перерізу повітряних ліній
- Вибір перерізу провідників у мережах напругою до 1000 В з урахуванням плавких запобіжників
- Вибір перерізу провідників у мережах напругою до 1000В з урахуванням автоматичних вимикачів і теплових реле
- Визначення площі перерізу арматури
- Визначення потрібної площі перерізу стояка.
- Визначення розмірів поперечного перерізу колони
- Внутрішні сили. Метод перерізів
- Геометричні характеристики деяких перерізів
- Геометричні характеристики поперечного перерізу
- Головні осі інерції та головні моменти інерції перерізу
- Головні осі інерції та головні моменти інерції перерізу
| <== попередня сторінка | | | наступна сторінка ==> |
| Циліндр. | | | Координати в просторі. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |