
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лабораторна робота № 2
Побудова двофакторної лінійної моделі продуктивності праці
Згідно варіанту завдання (дод. 1) побудувати двофакторну лінійну регресійну модель залежності продуктивності праці (Y, тис.грн./чол.) від втрат робочого часу, (Х1) та коефіцієнту використання потужностей (Х2 ). Необхідно:
1. Знайти параметри моделі.
2. Розрахувати коефіцієнти еластичності, кореляції та детермінації; стандартну та відносну похибки; критерій Фішера.
3. Представити модель на графіку, побудувавши поле кореляції та теоретичну лінію регресії.
4. Зробити загальний економічний аналіз моделі.
Розв’язання.
1. Економічний зміст змінних:
Y – продуктивність праці, тис.грн /чол. (залежна змінна);
Х1 – рівень втрат робочого часу, тис.люд.-год./рік (незалежна змінна);
Х2 – коефіцієнт використання потужностей, % (незалежна змінна).
2. Загальний вид лінійної форми економетричної моделі:
Y = а0 + а1Х1 + а2Х2 + u,
де а0, а1, а2 – параметри моделі; u – залишки, інші невраховані чинники.
2. Вихідні дані для розрахунків та побудови моделі наведені
в табл. 2.1.
Таблиця 2.1
| Спосте-реження | Функція | 1-й аргумент | 2-й аргумент |
| Y | X1 | X2 | |
| 13,1 | 8,3 | 55,8 | |
| 13,4 | 56,1 | ||
| 8,7 | 57,1 | ||
| 12,8 | 8,1 | 60,3 | |
| 14,5 | 7,5 | 61,4 | |
| 14,8 | 6,5 | 62,5 | |
| 15,1 | 70,4 | ||
| 15,4 | 5,9 | 71,7 | |
| 15,9 | 5,4 | 73,7 | |
| 16,3 | 5,1 | 73,7 | |
| 17,4 | 4,3 | 75,8 | |
| 18,1 | 2,1 | 76,7 | |
| 77,9 | |||
| 19,3 | 1,5 | 78,1 | |
| 19,3 | 1,5 | 78,1 |
4. Для визначення коефіцієнтів регресії а0, а1 та а2, складаємо систему нормальних рівнянь:
 а0 N + а1 åX1 + а2 å X2 = å Y
а0 N + а1 åX1 + а2 å X2 = å Y
а0 å X1 + а1 å(X1)2 + а2 å X1 X2 = å Y X1 (2.1)
а0 å X2 + а1 å X1 X2 + а2 å (X2)2 = å Y X2
де n – кількість спостережень, n = 15.
Всі суми обраховуються на основі вихідних статистичних даних
в таблиці 2.2.
5. На основі рівняння 2.1 та обрахованих сум в таблиці 2.2 запишемо для нашого прикладу:
 а0 ×15 + а1 × 80,9 + а2 × 1029,3 = 237,4
а0 ×15 + а1 × 80,9 + а2 × 1029,3 = 237,4
а0 × 80,9 + а1 × 530,07+ а2 × 5260,28 = 1196,84
а0 × 1029,3 + а1 × 5260,28 + а2 × 71690,15 = 16554,47
В результаті розв’язання системи отримуємо значення:
а0 = 18,052, a1 = –0,797, a2 = 0,03.
Таким чином, рівняння регресії буде мати вигляд:
Yрозр = 18,052 – 0,797 × Х1 + 0,03 × Х2 .
6. Визначимо коефіцієнти детермінації для даної моделі.
Для цього обчислимо дисперсії залежної змінної та залишків.
 ;
;
 .
.
 ;
;
 .
.
Таблиця 2.2
| спост | Yфакт | X1 | X2 | Y · X1 | Y · X2 | (X1)2 | (Х2)2 | Х1 · Х2 | Yрозр | (Yфакт–Yрозр)2 | (Yфакт –Yсер)2 |
| 13,1 | 8,3 | 55,8 | 108,7 | 731,0 | 68,9 | 3113,6 | 463,1 | 13,12 | 0,0005 | 7,43 | |
| 13,4 | 8,0 | 56,1 | 107,2 | 751,7 | 64,0 | 3147,2 | 448,8 | 13,37 | 0,0009 | 5,89 | |
| 13,0 | 8,7 | 57,1 | 113,1 | 742,3 | 75,7 | 3260,4 | 496,8 | 12,84 | 0,0249 | 7,99 | |
| 12,8 | 8,1 | 60,3 | 103,7 | 771,8 | 65,6 | 3636,1 | 488,4 | 13,42 | 0,3811 | 9,16 | |
| 14,5 | 7,5 | 61,4 | 108,8 | 890,3 | 56,3 | 3770,0 | 460,5 | 13,93 | 0,3261 | 1,76 | |
| 14,8 | 6,5 | 62,5 | 96,2 | 925,0 | 42,3 | 3906,3 | 406,3 | 14,76 | 0,0016 | 1,05 | |
| 15,1 | 6,0 | 70,4 | 90,6 | 1063,0 | 36,0 | 4956,2 | 422,4 | 15,40 | 0,0881 | 0,53 | |
| 15,4 | 5,9 | 71,7 | 90,9 | 1104,2 | 34,8 | 5140,9 | 423,0 | 15,52 | 0,0134 | 0,18 | |
| 15,9 | 5,4 | 73,7 | 85,9 | 1171,8 | 29,2 | 5431,7 | 398,0 | 15,97 | 0,0056 | 0,01 | |
| 16,3 | 5,1 | 73,7 | 83,1 | 1201,3 | 26,0 | 5431,7 | 375,9 | 16,21 | 0,0074 | 0,22 | |
| 17,4 | 4,3 | 75,8 | 74,8 | 1318,9 | 18,5 | 5745,6 | 325,9 | 16,92 | 0,2349 | 2,48 | |
| 18,1 | 2,1 | 76,7 | 38,0 | 1388,3 | 4,4 | 5882,9 | 161,1 | 18,70 | 0,3557 | 5,17 | |
| 19,0 | 2,0 | 77,9 | 38,0 | 1480,1 | 4,0 | 6068,4 | 155,8 | 18,81 | 0,0352 | 10,07 | |
| 19,3 | 1,5 | 78,1 | 29,0 | 1507,3 | 2,3 | 6099,6 | 117,2 | 19,22 | 0,0069 | 12,06 | |
| 19,3 | 1,5 | 78,1 | 29,0 | 1507,3 | 2,3 | 6099,6 | 117,2 | 19,22 | 0,0069 | 12,06 | |
| S | 237,4 | 80,9 | 1029,3 | 1196,84 | 16554,4 | 530,07 | 71690,1 | 5260,28 | 237,40 | 1,49 | 76,07 |
Коефіцієнт детермінації буде дорівнювати:
 ;
;
 .
.
Отриманий коефіцієнт детермінації R2 = 0,977 свідчить про те, що варіація рівня продуктивності праці на 97,7 % визначається варіацією незалежних змінних Х1 та Х2 і лише 2,3 % змін Y припадає на невраховані чинники.
7. Оцінка точності по середньоквадратичній похибці:

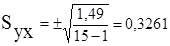
8. Відносна похибка:
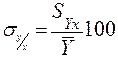

9. Оцінка достовірності по розрахунковому критерію Фішера
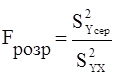
Fрозр. = 76,07: 1,49 = 51,08
Порівнюємо розрахункове значення критерію Фішера з табличним:
F95табл. = 2,5 ;
Fрозр. > F95табл.
Модель приймаємо – припускаємо присутність лінійного зв'язку.
10. Коефіцієнт множинної кореляції
 ;
;
 , що свідчить про вельми високий зв’язок між показниками Y та X1 , X2 .
, що свідчить про вельми високий зв’язок між показниками Y та X1 , X2 .
11. Коефіцієнт регресії а1 = – 0,797 показує, що зниження втрат робочого часуна 1 тис. год./рік може привести до роступродуктивностіпраці на 0,797 тис.грн./чол.
Коефіцієнт регресії а2 = 0,03 показує, що підвищення коефіцієнту використання потужності на 1% може привести до росту продуктивності праці на 0,03 тис.грн./чол.
12. Графічне відображення моделі базується на побудові ліній регресії у прямокутних координатах Y-Х1 та Y-Х2. При цьому масштаб необхідно вибрати таким, щоб мінімальні і максимальні значення X1 та X2 співпадали між собою.
| X1 | X2 | Y=f(X1) при X2= const | Y=f(X2) при X1= const | Середнє значення | ||
| X1 | X2 | |||||
| min | 1,50 | 55,80 | 18,93 | 15,44 | 5,39 | 68,62 |
| max | 8,70 | 78,10 | 13,19 | 16,11 |

13. Відносна зміна залежної змінної Y в процентах при зміні на 1% аргументів Х1 та Х2 характеризують коефіцієнти еластичності Е1 та Е2, які розраховуються за наступною формулою:
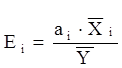
де аі – коефіцієнт регресії при і-тому факторі;
 – середнє значення і-тої незалежної змінної (фактора);
– середнє значення і-тої незалежної змінної (фактора);
 – середнє значення залежної змінної (розрахункове).
– середнє значення залежної змінної (розрахункове).


Розраховані коефіцієнти еластичності дають можливість побудувати графік еластичності:
| Х1 (%) | Y1 (%) | Х2 (%) | Y2 (%) |
| –0,27 | 0,13 | ||
| –0,54 | 0,26 |

14. Порівняємо дві моделі (лаб.№1 та лаб. №2)
Коефіцієнти кореляції r = 0,9879 та r = 0,9902 свідчать про те, що залучення другої змінної Х2 збільшує тісноту зв’язку між залежною і факторами. Середньоквадратична похибка зменшилася з 0,3413 до
0,3261 тис.грн./рік. Відносна похибка зменшилась з 2,157% до 2,06%.
15. Висновок.
З аналізу одержаної моделі залежності продуктивності праці від втрат робочого часу і коефіцієнту використання потужності можна зробити висновок, що модель достовірна і може бути використана для кількісного практичного економічного висновку.
На даному підприємстві збільшення продуктивність праці обумовлюється зменшенням втрат робочого часу. Так, при зменшенні втрат робочого часу на кожну 1 тис.год./рік, продуктивність праці збільшиться на 0,797 тис.грн./чол.
При збільшенні коефіцієнту використання потужності на 1% продуктивність праці зросте на 0,03 тис.грн./чол.
Читайте також:
- II. Будова доменної печі (ДП) і її робота
- II. Самостійна робота студентів.
- IV. ВИХОВНА РОБОТА В КЛАСІ
- IV. ІНДИВІДУАЛЬНА РОБОТА СТУДЕНТІВ.
- IV. Науково-дослідницька робота.
- IV. Практична робота.
- IV. Робота над темою уроку
- Qорганізаційне середовище, в якому виконується робота
- V. Робота з підручником
- V. Робота з підручником. с. 59-60
- V. Робота з програмою «Виконавець Восьминіжка»
- V. Робота з програмою «Виконавець Садівник».
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Тема: «Методи Побудови множинних економетричних моделей» |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |