• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Параметри статистичних розподілів

Величина 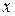, що є результатом досліду, як правило є випадковою величиною, тобто заздалегідь непередбачувана і міняється від досліду до досліду. Провівши дослід нескінченне велике число разів, ми отримаємо генеральну сукупність - повний набір всіх значень, які може приймати випадкова величина. У реальних умовах дослід проводиться кінцеве число разів і ми отримуємо вибірку, що складається з кінцевого числа значень випадкової величини. Це число називається об'ємом вибірки. Генеральна сукупність - граничний випадок вибірки з нескінченно великим об'ємом. Між параметрами вибірки і параметрами генеральної сукупності є принципова відмінність. Якщо узяти декілька вибірок одного і того ж об'єму n, тобто провести декілька серій дослідів або вимірювань n дослідів в кожній серії, то, через випадковий характер вимірюваних величин, параметри вибірок відрізнятимуться один від одного. Іншими словами, параметри серій вимірювань (наприклад, середні значення результатів вимірювань в серії) є випадковими навіть за незмінних умов досліду. Параметри ж генеральної сукупності за заданих умов досліду незмінні. Тому спочатку розглянемо параметри генеральної сукупності, які математично описуються простіше, ніж параметри вибірки.

Параметри генеральної сукупності:

1.Середнє значення (або математичне очікування ( ))

. (1)

Середнє значення, що відповідає нескінченному числу вимірювань, позначатимемо , щоб відрізнити його від середнього значення 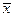, що відповідає серії з n вимірювань. У відсутність систематичних похибок воно співпадає з дійсним значенням вимірюваної величини.

2. Дисперсія - середній квадрат відхилення випадкової величини від середнього значення

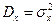= (2)

3. Середньоквадратичне (стандартне) відхилення 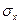, що характеризує розкид випадкових величин:

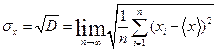(3)

Величину 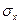називають також середньоквадратичною похибкою або стандартом даного розподілу.

При обробці результатів вимірювань важливе значення має закон додавання дисперсій :

.

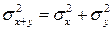Він завжди використовується тоді, коли потрібно визначити похибки результату, обумовленого сукупністю різних незалежних факторів.

Читайте також:

1. Алгоритм виконання непараметричного тестів Спірмана та Кендалла у програмному комплексі SPSS (Statistica)
2. Аналіз статистичних даних про склад та плинність кадрів, які обіймали керівні
3. Аналіз статистичних залежностей періодичних відліків часу ПФС від температури
4. Аналітичні параметри
5. Аналітичні параметри
6. Антропометричні параметри людини, які використовуються в ергономіці (см)
7. Артеріальний пульс, основні параметри
8. Артеріальний пульс, основні параметри
9. Болтове рознімне з’єднання та його параметри
10. Будова, характеристики і параметри біполярного транзистора
11. Варіатори та їхні основні параметри
12. Векторне канонічне параметричне рівняння прямої в просторі.

Переглядів: 567