• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Методичні вказівки

Міністерство освіти України

Чернівецький державний університет імені Юрія Федьковича

ЦИФРОВА ОБРОБКА ІНФОРМАЦІЇ

І РОЗПІЗНАВАННЯ ОБРАЗІВ

МЕТОДИЧНІ ВКАЗІВКИ І ЗАВДАННЯ

ДО ЛАБОРАТОРНИХ РОБІТ

Для студентів математичного факультету

спеціальності “Інформатика”

Чернівці

ЧДУ

УДК 681.3.019:621.398

Методичні вказівки і завдання до лабораторних робіт з курсу “Цифрова обробка інформації і розпізнавання образів” /Укл.: Сопронюк Ф.О., Гайдайчук І.В., Фратавчан В.Г. – Чернівці: ЧДУ, 1999. – 36 с.

Друкується за ухвалою редакційно-видавничої ради Чернівецького державного університету імені Юрія Федьковича

Укладачі: Сопронюк Федір Олексійович, доктор фізико-математичних наук, професор (відповідальний за випуск),

Гайдайчук Ігор Васильович, Фратавчан Валерій Григорович, кандидати фізико-математичних наук, асистенти;

Підписано до друку 18.11.99. Формат 60x84/16.

Папір газетний. Друк офсетний. Ум. друк. арк. 1.7. Обл.-вид. арк. 1.8

Зам. 349. Тираж 100 прим.

Друкарня видавництва “Рута” Чернівецького держуніверситету

274012, Чернівці, вул. Коцюбинського, 2

Вступ

Запропоновані методичні вказівки і завдання до лабораторних робіт відповідають курсу “Цифрова обробка інформації і розпізнавання образів”, який читається для студентів п’ятого курсу спеціальності “Інформатика”. Вони покликані допомогти студентам денної та заочної форм навчання більш глибоко засвоїти лекційний матеріал і навчитися застосовувати набуті знання для фільтрації сигналів, кодування та стиснення інформації, розпізнавання конкретних об’єктів.

Структура та зміст даної розробки відповідають вимогам “Освітньо-професійної програми вищої освіти України”. До її складу увійшли такі теми:

· швидке перетворення Фур’є;

· алгоритми стиснення даних;

· розпізнавання бінарних образів;

· використання перетворення Фур’є у розпізнаванні зображень;

· корекція помилок при передачі інформації.

Вказані теми охоплюють майже весь лекційний матеріал, передбачений програмою для вищих навчальних закладів. До кожної з них наведені відповідні теоретичні обгрунтування, деякі ілюструються розв’язаннями типових прикладів, запропоновані варіанти завдань для самостійної роботи і перерахована допоміжна література.

Лабораторна робота № 1

Швидке перетворення Фур’є (ШПФ)

Література: [1,2,3,4,8,11].

Мета роботи:Програмно реалізувати швидке дискретне перетворення Фур’є .

Зміст роботи: За заданими відліками функції обчислити коефіцієнти її розкладу в ряд Фур’є, здійснити низькочастотну фільтрацію і зобразити на екрані отриманий сигнал.

Методичні вказівки

Перетворення Фур’є.При розв’язуванні багатьох задач математики та фізики необхідно здійснити розклад періодичної функції з періодом 2p в ряд Фур’є

. (1.1)

Тригонометричний многочлен

збігається в середньоквадратичному до , якщо

, , , (1.2)

Якщо деяка функція задана на інтервалі , то її розклад у ряд Фур’є має такий вигляд:

, (1.3)

де

, , , (1.4)

— основна частота розкладу.

Ряд (1.1) можна записати у вигляді

, (1.5)

де , , або , (1.6)

де (1.7)

Дискретне перетворення Фур’є.Нехай деяка функція на відрізку відома тільки в дискретній системі точок , , тобто відомі відліки . Позначимо 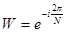, де - основна частота, . Тоді

, (1.8)

де

, (1.9)

.

Перетворення (1.9) називається дискретним перетворенням Фур’є, при обчисленні якого потрібно використати порядку множень і додавань. У випадку, коли є складеним числом, існує декілька алгоритмів для пришвидшення обчислень. Ці методи отримали назву швидкого перетворення Фур’є. Розглянемо алгоритми, які використовують перехід від одновимірного до двовимірного перетворення Фур’є.

Алгоритм Кулі-Тьюкі. Для його пояснення припустимо, що . Тоді, перепозначивши 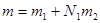і , де , , , , запишемо (1.9) у вигляді

. (1.10)

У формулі (1.10) не більше комплексних множень і комплексних додавань.

Остаточно алгоритм Кулі-Тьюкі формулюється так:

1. Записуємо вхідні дані для алгоритму (відліки) у вигляді матриці .

2. Виконуємо -точкове перетворення Фур’є по стовпцях, тобто домножуємо на відповідні . Результати записуємо у цю ж таблицю.

3. Обчислюємо 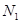-точкове перетворення Фур’є по рядках і записуємо результат у таблицю.

4. Переходимо від таблиці до вектора розміру .

Особливо відмітимо випадок, коли , де 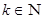-множини натуральних чисел. Тоді алгоритм можна записати рекурсивно. Якщо комплексне множення реалізувати через чотири дійсні множення і два дійсних додавання, то загальна кількість дійсних множень дорівнює , а дійсних додавань — .

Алгоритм Гуда-Томаса. Як і в методі Кулі-Тьюки, припускаємо, що , але додатково вимагатимемо, щоб 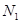і були взаємно простими. Індекси у двовимірній таблиці задаються за правилами , . З китайської теореми про лишки випливає існування таких чисел і , що виконується рівність , де . Вихідні індекси у результуючому одновимірному векторі визначаються дещо інакше. Нехай , . Перепишемо ці рівності в еквівалентному вигляді

,

.

Тоді вихідні індекси обчислюються за правилом . У цих нових індексних позначеннях формула (1.9) набуває вигляду

.

Виконаємо множення у показнику степеня. Оскільки порядок елемента дорівнює , то члени з цим показником дорівнюють 1. Тоді описане вище перетворення індексів для елементів вхідної і вихідної таблиць дає

, (1.11)

де і . Елементи і є тепер простими коренями з одиниці степенів 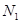і , що задають відповідно 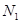-точкове і -точкове перетворення Фур’є. Отже, рівняння (1.11) записано тепер у формі двовимірного -точкового перетворення Фур’є. Кількість множень і кількість додавань приблизно дорівнює .

В обох методах перетворення Фур’є по рядках і по стовпцях,

якщо відповідна вимірність задається складеним числом, можна у свою чергу спростити, застосовуючи алгоритм ШПФ.

Завдання для самостійної роботи

На відрізку задана функція . Необхідно:

· рівномірно розбити відрізок вузлами, обчислити відліки функції у вибраних точках, намалювати графік функції;

· обчислити коефіцієнти Фур’є , ;

· обчислити перетворення Фур’є , намалювати графік.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

21. .

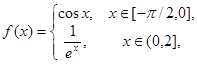
22. .

23. .

24. .

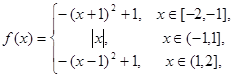
25. .

26. .

Читайте також:

1. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
2. II. МЕТОДИЧНІ ВКАЗІВКИ
3. V. ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ
4. VIІ. Короткі методичні вказівки до роботи студентів на практичному занятті
5. В ході аудиту фінансової звітності аудитором застосовуються методичні прийоми документального та фактичного контролю.
6. ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНИХ РОБІТ
7. Вказівки до виконання контрольної роботи
8. ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ
9. Вказівки до виконання контрольної роботи
10. Вказівки до виконання контрольної роботи ( РГР ).
11. Вказівки до виконання контрольної роботи ( РГР ).
12. Вказівки до компоновки міжповерхового Перекриття

Переглядів: 671