• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Лекція 3. Машини з натуральнозначними регістрами.

План:

1.Поняття про МНР.

2.Структура та система команд МНР.

3.Приклади роботи МНР.

4.МНР обчислюванні функції .

Література: [2], [4], [10].

Машина з натуральнозначними регістрами (МНР) є ідеалізованою моделлю комп'ютера. МНР містить нескінчену кількість регістрів, вмістом яких є натуральні числа. Регістри нумеруємо (іменуємо) натуральними числами, починаючи з 0, і позначаємо їх R₀,R₁,…,R_n,… . Вміст регістра R_n

позначатимемо ^’R_n. Послідовність (^’R₀,^’R₁,...,^’R_n,...) вмістів усіх регістрів МНР називатимемо конфігурацією МНР.

МНР може змінити вміст регістрів згідно виконуваної нею команди. Скінчений список команд утворює програму МНР. Команди програми послідовно нумеруємо (іменуємо) натуральними числами, починаючи з 1. МНР-програму з командами І_1, І₂,...,І_k будемо позначати P=І₁І₂…I_k. Довжину (кількість команд) МНР-програми Р позначатимемо |Р|.

Команди МНР бувають 4-х типів :

Тип 1. Обнулення n-го регістру Z(n): ^’R_n=0.

Тип 2. Збільшення вмісту n-го регістру на одиницю S(n): ^’R_n= ^’R_n+1.

Тип 3. Переадресація Т(m,n): ^’R_n:= ^’R_m (при цьому ^’R_m не змінюється).

Команди типів 1-3 називають арифметичними. Після виконання арифметичної команди МНР повинна виконувати наступну за списком команду програми.

Тип 4. Умовний перехід J(m,n,q) : якщо ^’R_n= ^’R_m , то перейти на виконання q-ї команди, інакше виконувати наступну за списком команду програми.

Виконання програми МНР починає, перебуваючи в деякій початковій конфігурації, з виконання першої за списком команди. Тобто, всі початкові дані задаються в ручну перед початком виконання програми. Домовимось, що всі вхідні дані алгоритму розміщуємо у перших послідовних регістрах, а результат виконання алгоритму (якщо він скалярний) розміщуємо у нульовому регістрі. Наступна для виконання команда програми визначається так, як описано вище. Виконання програми завершується (програма зупиняється), якщо наступна для виконання команда відсутня (тобто номер наступної команди перевищує номер останньої команди програми). Конфігурація МНР в момент завершення виконання програми називається фінальною і вона визначає результат роботи МНР- програми над даною початковою конфігурацією.

Якщо МНР-програма Р при роботі над початковою конфігурацією (а₀,а₁,...) зупиняється із фінальною конфігурацією (b₀,b₁,...), це позначають наступним чином: Р(а₀,а₁...)*(b₀,b₁,...). Якщо МНР-програма Р при роботі над початковою конфігурацією ніколи не зупиняється, це позначатимемо Р(а₀,а₁...)*. Домовимося також конфігурації виду (а₀,а₁...,а_n,0,0,...), в якій ^’R_m=0 для всіх m>n, позначати (а₀,а₁...,а_n).

Дві МНР-програми називаються еквівалентними, якщо при роботі над однаковими початковими конфігураціями вони або зупиняються з однаковими фінальними конфігураціями, або обидві не зупиняються.

МНР-програма Р вважається стандартною, якщо для кожної команди виду J(m,n,q) виконується умова q |P|+1.

Конкатенацією стандартних МНР-програм Р=І₁І₂...І_к та Q=I₁I₂…I_m назвемо стандартну МНР-програму І₁І₂...І_кІ_k+1...І_k+m , де команди І_к+1...І_к+m сспівпадають з командами програми Q, але кожна команда виду J(m,n,q) замінена командою J(m,n,q+к).

МНР-програма Р обчислює часткову функцію f : N^к → N, якщо Р(а₀,а₁...) * (b₀,b₁,...) тоді і тільки тоді, коли (а₀,а₁,...,а_n) D_f та f(а₀,а₁...,а_n)= b₀. Це означає, що значення аргументів функції послідовно розміщуються в послідовних перших регістрах, починаючи з R₀, а значення функції знімається з регістра R_0.

Функцію називають МНР-обчислюваною, якщо існує МНР-програма яка обчислює цю функцію.

Роглянемо ряд прикладів МНР-програм для найпростіших функцій.

Приклад 1. МНР-програма для функції f(x,y) = х+у :

Початкова конфігурація алгоритму ^’R₀=x, ^’R₁=y.

1) J(2,1,5)

2) S(0)

3) S ( 2 )

4) J ( 1,1,1 ).

Нехай Р - стандартна МНР-програма для n-арної функції f. Через Р[k₁k₂...k_n → r] позначимо МНР-програму виду :

Т(i,k_i-1) 1 і n

Z(k) n k (P)

P

T(0,r).

Тут (Р) - найбільший номер регістру, задіяного при обчисленні f (вважаємо (Р) 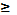n-1). Така МНР-програма обчислює функцію f, для випадку коли початкові значення аргументів занести в регістри k₁<...<k_n, а значення функції знімаються з регістру r. При цьому задіяні щонайбільше (Р)+1 регістр, із 0-го по (Р)-й.

Читайте також:

1. II. Регламент переговоров и действий машиниста и помощника машиниста
2. Аеродинамічні властивості колісної машини
3. Аналогові обчислювальні електронні машини.
4. БАГАТОКОВШОВІ ЕКСКАВАТОРИ. ВИЙМАЛЬНО-ТРАНСПОРТУЮЧІ МАШИНИ. КОМПЛЕКСИ МАШИН БЕЗПЕРЕРВНОЇ ДІЇ
5. Блок 3.2. Лекція 9. Небезпеки техногенного характеру
6. Будова й основні елементи машини
7. Вид заняття: лекція
8. Вид заняття: лекція
9. Вид заняття: лекція
10. Вид заняття: лекція
11. Вид заняття: лекція
12. ВИЗНАЧЕННЯ ОБЛАСТІ ОПТИМАЛЬНОГО ВИКОРИСТАННЯ КОМПЛЕКТІВ МАШИНИ

Переглядів: 1959