• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення

Алгебра множин

Пріоритет операцій, тотожності алгебри множин, тотожні перетворення виразів

Множина 2^U всіх підмножин універсальної множини U із заданими на ньому чотирма операціями складає алгебру множин.

У загальному випадку алгебру може складати будь-який клас crÌ 2^U підмножин універсальної множини U, замкнений відносно всіх чотирьох операцій (див. п. 4.8). Визначення алгебри, що не містить надмірних (точніше, залежних) обмежень, виглядає таким чином.

Клас множин crназивається алгеброю (множин), якщо:

1. U Î cr.

2. З А, В Î crвиходить A È В Îcr.

3. З А, В Î crвиходить А\В Îcr.

Алгебра множин широко застосовується у програмуванні, зокрема, при роботі з різноманітними базами даних і становить основу для побудови багатьох математичних структур. Разом з тим, що алгебра множин має основоположне значення в математиці, вона дуже проста і близька до реального життя. Ми щодня застосовуємо операції та закони алгебри множин, не замислюючись над цим. Ми відраховуємо з множин задач, які потрібно розв'язати, множину розв'язаних та беремося до розв'язання решти. Із них ми, вірогідно, в першу чергу виберемо ті, які відносяться до множини легких. Ми готуємо сніданок, визначаючи перетин множини наявних продуктів з множиною продуктів, які нам подобаються. Все наше життя проходить серед множин, які якось взаємозв'язані.

Ми маємо достатньо операцій, щоб створювати складні алгебраїчні вирази. Для цього необхідно визначити, який пріоритет мають операції відносно одна до одної.

Пріоритет операцій в алгебрі множин такий:

1. .

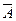2. A Ç B .

3. A È B .

4. А\В.

Розглянемо приклад.

Приклад. Нехай треба розташувати дужки (визначити послідовність виконання операцій) у формулі:

.

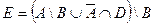З урахуванням пріоритетів це слід зробити так:

.

В алгебрі множин crавтоматично виконуються такі тотож­ності, які дозволяють віднести crдо класу так званих булевих алгебр(див. розділ 4):

1. Комутативні закони

1.1. .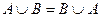

1.2. .

2.Асоціативні закони

2.1..

2.2..

3. Дистрибутивні закони

3.1..

3.2..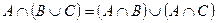

4. Властивості порожньої та універсальної множин

4.1. A È Æ = А.

4.2. A Ç U = A.

4.3. A È U = U

4.4. А Ç Æ = Æ.

5. Закони ідемпотентності

5.1. A È A = А

5.2. А Ç А = А.

6. Закон інволюції

.

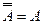7. Закон протиріччя

Æ.

8. Закон виключеного третього

.

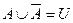9. Закон елімінації

9.1.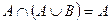

9.2. .

10. Закони де Моргана

10.1.

10.2..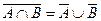

Усі наведені тотожності можна наочно зобразити і довести, використовуючи діаграми Венна.

Приклад.Довести за допомогою діаграм Венна дистрибутивний закон 3.2.

.

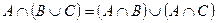Проілюструємо на діаграмі ліву частину тотожності, виконавши спочатку об'єднання множин В і С, а потім перетин зА (рис. 1.11).

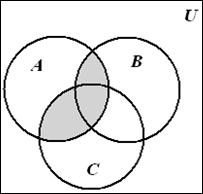
ВÈС АÇ(ВÈС)

Рис. 1.11 Побудова діаграми Венна для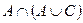

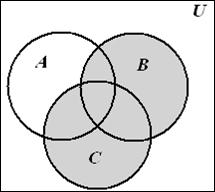
Тепер побудуємо діаграму для правої частини тотожності - (рис. 1.12.)

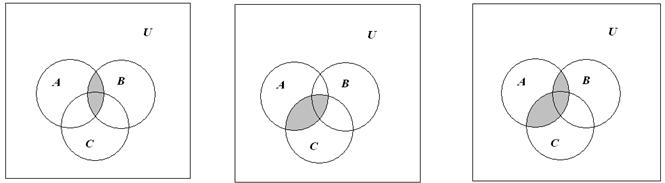
Рис. 1.12 Побудова діаграми Венна для

Як бачимо, праві діаграми на рис. 1.11і 1.12співпадають, отже тотожність 3.2 справедлива.

За допомогою тотожностей алгебри множин можна здійснювати еквівалентні перетворення виразів - Розглянемо такі перетворення на прикладі.

Приклад.Спростити вираз

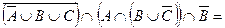(застосуємо закон де Моргана)

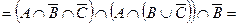(асоціативність і комутативність)

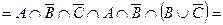(застосуємо закон ідемпотентності)

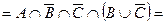(застосуємо дистрибутивний закон)

(згідно з властивостями порожньої множини)

= Æ .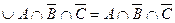

Відповідь: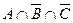

Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. Ocнoвнi визначення здоров'я
5. Алгебраїчний спосіб визначення точки беззбитковості
6. Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
7. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
8. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
9. Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
10. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
11. Біостратиграфічні методи визначення віку порід
12. Біуретовий метод визначення білків

Переглядів: 869